Chào mừng bạn đến với bài giải chi tiết Bài 3 trang 175 Tài liệu dạy – học Toán 7 tập 1 trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải dễ hiểu, phương pháp giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 7.
Bài 3 thuộc chương trình Toán 7 tập 1, tập trung vào việc... (phần này sẽ được điền nội dung cụ thể về chủ đề bài 3)
Giải bài tập Cho tam giác ABC nhọn. Về phía ngoài tam giác ABC vẽ tam giác BAD vuông cân tại A, tam giác CAE vuông cân tại A. Chung minh rằng :
Đề bài
Cho tam giác ABC nhọn. Về phía ngoài tam giác ABC vẽ tam giác BAD vuông cân tại A, tam giác CAE vuông cân tại A. Chung minh rằng :
a) DC = BE.
b) \(DC \bot BE.\)
c) \(B{D^2} + C{E^2} = B{C^2} + D{E^2}.\)
Lời giải chi tiết
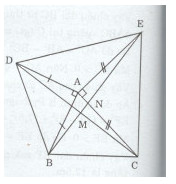
a)Ta có: \(\eqalign{ & \widehat {BAE} = \widehat {CAE} + \widehat {BAC} = {90^0} + \widehat {BAC} \cr & \widehat {DAC} = \widehat {DAB} + \widehat {BAC} = {90^0} + \widehat {BAC} \cr} \)
Nên \(\widehat {BAE} = \widehat {DAC}\)
Xét hai tam giác ADC và ABE có:
AD = AB (tam giác BAD vuông cân tại A)
\(\widehat {DAC} = \widehat {BAE},AC = AE(\Delta CAE\) vuông cân tại A)
Do đó: \(\Delta ADC = \Delta ABE(c.g.c) \Rightarrow CD = BE.\)
b) Gọi M, N lần lượt là giao điểm của BE với CD, AC.
Ta có: \(\widehat {ANE} + \widehat {AEN} = {90^0}(\Delta ANE\) vuông tại A).
Mà \(\widehat {ANE} = \widehat {MNC}\) (đối đỉnh), \(\widehat {AEN} = \widehat {MCN}(\Delta ADC = \Delta ABE)\)
Suy ra \(\widehat {MNC} + \widehat {MCN} = \widehat {ANE} + \widehat {AEN} = {90^0}.\)
Tam giác CMN có: \(\widehat {NMC} + \widehat {MNC} + \widehat {MCN} = {180^0}\)
Do đó: \(\widehat {NMC} = {180^0} - {90^0} = {90^0}.\) Vậy \(CD \bot BE.\)
Tam giác MBD vuông tại M \(\Rightarrow B{D^2} = M{B^2} + M{D^2}\) (định lí Pythagore)
Tam giác MCE vuông tại M \(\Rightarrow C{E^2} = M{C^2} + M{E^2}\) (định lí Pythagore)
Do đó: \(B{D^2} + C{E^2} = M{B^2} + M{D^2} + M{C^2} + M{E^2}(1)\)
Tam giác MBC vuông tại M \(\Rightarrow B{C^2} = M{B^2} + M{C^2}\) (định lí Pythagore)
Tam giác MDE vuông tại M \(\Rightarrow D{E^2} = M{D^2} + M{E^2}\) (định lí Pythagore)
Do đó: \(B{C^2} + D{E^2} = M{B^2} + M{C^2} + M{D^2} + M{E^2}(2)\)
Tà (1) và (2) ta có: \(B{D^2} + C{E^2} = B{C^2} + D{E^2}\)
Bài 3 trang 175 Tài liệu dạy – học Toán 7 tập 1 là một bài tập quan trọng trong chương trình học Toán 7. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về... (nêu kiến thức liên quan). Để giúp các em học sinh hiểu rõ hơn về bài tập này, giaitoan.edu.vn xin trình bày lời giải chi tiết và hướng dẫn giải bài tập như sau:
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các kiến thức sau:
Đề bài: (Viết lại đề bài đầy đủ)
Lời giải:
Kết luận: (Nêu kết luận của bài toán)
Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xem xét một số ví dụ minh họa sau:
(Đề bài ví dụ 1)
(Lời giải ví dụ 1)
(Đề bài bài tập tương tự)
(Gợi ý giải bài tập tương tự)
Ngoài cách giải trên, chúng ta có thể tiếp cận bài toán này bằng một phương pháp khác. Phương pháp này dựa trên... (giải thích phương pháp khác).
Để củng cố kiến thức và kỹ năng giải bài tập, các em học sinh có thể tự luyện tập thêm với các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập Bài 3 trang 175 Tài liệu dạy – học Toán 7 tập 1, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin giải các bài tập Toán 7 khác. Chúc các em học tập tốt!
| STT | Nội dung | Giải thích |
|---|---|---|
| 1 | ... | ... |
| 2 | ... | ... |