Chào mừng các em học sinh đến với lời giải chi tiết bài 1.22 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức trên giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
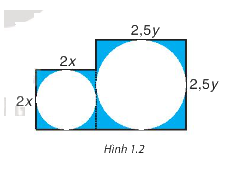
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimet và y centimet.
Đề bài
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimet và y centimet. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimet) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Biểu thị diện tích phần còn lại của miếng bìa: Diện tích phần còn lại = Diện tích 2 hình vuông – Diện tích 2 hình tròn.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Lời giải chi tiết
Diện tích hai hình vuông là: \(2x.2x + 2,5y.2,5y = 4{x^2} + 6.25{y^2}\)
Diện tích hai hình tròn là: \({\pi .{x^2} + \pi .{y^2}}\)
Diện tích phần còn lại của miếng bìa là:
\(\begin{array}{l}S = 4{x^2} + 6.25{y^2} - \pi .{x^2} - \pi .{y^2}\\ = \left( {4 - \pi } \right){x^2} + \left( {6,25 - \pi } \right){y^2}\end{array}\)
Biểu thức này là một đa thức, có bậc là 2.
Bài 1.22 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về đa thức, thu gọn đa thức và tìm bậc của đa thức. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc biến đổi đa thức.
Bài tập yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài tập này, chúng ta cần thực hiện theo các bước sau:
a) Tìm bậc của đa thức 5x4 - 3x3 + x2 - 5x + 1:
Đa thức có các số hạng: 5x4, -3x3, x2, -5x, 1. Số hạng có bậc cao nhất là 5x4 với bậc là 4. Vậy, bậc của đa thức là 4.
b) Tìm bậc của đa thức -2x5 + 3x2 - 7:
Đa thức có các số hạng: -2x5, 3x2, -7. Số hạng có bậc cao nhất là -2x5 với bậc là 5. Vậy, bậc của đa thức là 5.
c) Tìm bậc của đa thức 4x - 5x3 + 2x5 - x2:
Đa thức có các số hạng: 4x, -5x3, 2x5, -x2. Số hạng có bậc cao nhất là 2x5 với bậc là 5. Vậy, bậc của đa thức là 5.
a) Thu gọn đa thức 3x2 + 2x - 5x2 + 7x - 2:
Thu gọn các số hạng đồng dạng: (3x2 - 5x2) + (2x + 7x) - 2 = -2x2 + 9x - 2. Vậy, đa thức thu gọn là -2x2 + 9x - 2.
b) Thu gọn đa thức x3 - 2x2 + 5x + x2 - x3 + 4x:
Thu gọn các số hạng đồng dạng: (x3 - x3) + (-2x2 + x2) + (5x + 4x) = 0x3 - x2 + 9x = -x2 + 9x. Vậy, đa thức thu gọn là -x2 + 9x.
Việc giải bài tập về đa thức không chỉ giúp học sinh nắm vững kiến thức về đa thức mà còn là nền tảng quan trọng cho các bài học tiếp theo trong chương trình Toán 8 và các chương trình Toán nâng cao. Kỹ năng thu gọn đa thức và tìm bậc của đa thức được ứng dụng rộng rãi trong việc giải các phương trình, bất phương trình và các bài toán thực tế.
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 1.22 trang 18 SGK Toán 8 tập 1 - Kết nối tri thức trên giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt nhất.