Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 80, 81, 82 sách giáo khoa Toán 8 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho tam giác ABC và các điểm M, N
Video hướng dẫn giải
Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC.
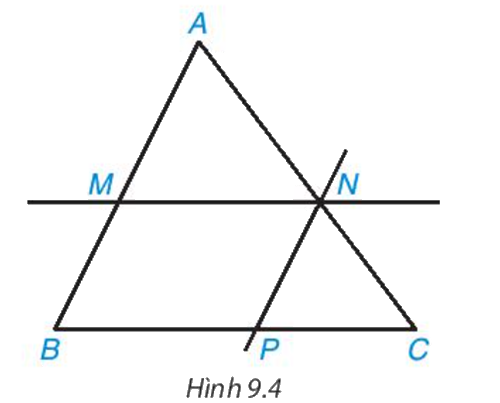
- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau
- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN=BP và suy ra \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng
Phương pháp giải:
Quan sát hình 9.4 để thực hiện các hoạt động.
Lời giải chi tiết:
- Các cặp góc bằng nhau của hai tam giác ABC và AMN: \(\widehat B = \widehat M{,^{}}\widehat C = \widehat N\)
- Có MN // BP, MB // NP (vì AB // NP) => MN=BP \( \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\)=> ΔABC \(\backsim\) ΔAMN
Video hướng dẫn giải
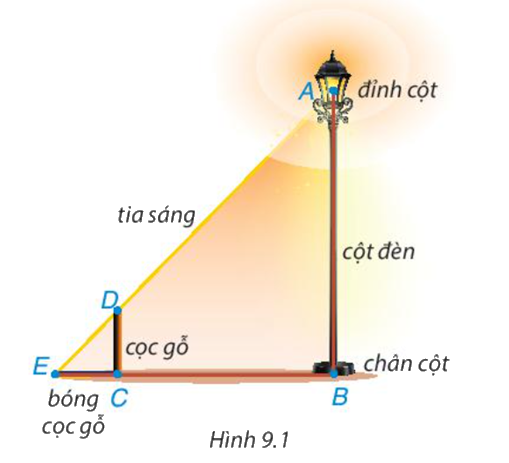
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Hãy giải thích bác Dương đã tính được chiều cao cột đèn như thế nào, biết cọc gỗ cao 1m, EC=80cm và EB=4m.
Phương pháp giải:
Dựa vào định lí ΔAEB \(\backsim\) ΔDEC và tìm tỉ số đồng dạng của chúng từ đó tính được chiều cao của cột đèn
Lời giải chi tiết:
Có EB=4m=400cm, CD=1m=100cm
Vì cọc gỗ và cột đèn đều thẳng đứng
=> AB // DC => ΔAEB \(\backsim\) ΔDEC \( \Rightarrow \frac{{DE}}{{A{\rm{E}}}} = \frac{{CE}}{{BE}} = \frac{{DC}}{{AB}}\)
Mà \(\frac{{CE}}{{A{\rm{E}}}} = \frac{{80}}{{100}} = \frac{1}{5}\)
=> Hai tam giác đồng dạng với tỉ số đồng dạng là \(\frac{1}{5}\)
\( \Rightarrow \frac{{DC}}{{AB}} = \frac{{100}}{{AB}} = \frac{1}{5}\)
=> AB=500cm=5m
Vậy cột đèn cao 5m
Video hướng dẫn giải
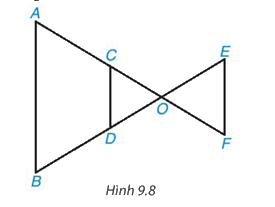
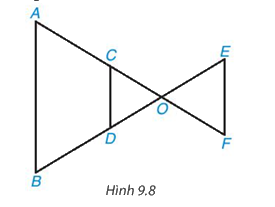
Trong hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.
Phương pháp giải:
Quan sát hình 9.8 để kể tên các tam giác đồng dạng
Lời giải chi tiết:
ΔOCD \(\backsim\) ΔOAB
ΔOEF \(\backsim\) ΔODC
ΔOEF \(\backsim\) ΔOBA
Video hướng dẫn giải
Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC.
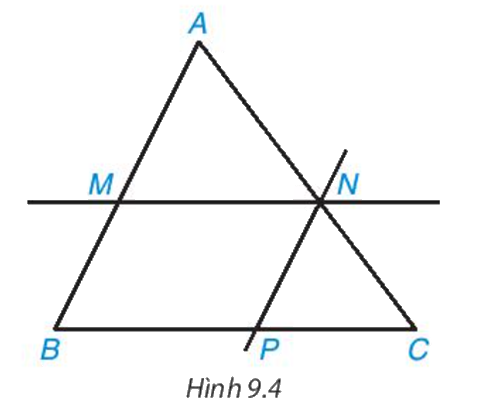
- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau
- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN=BP và suy ra \(\frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng
Phương pháp giải:
Quan sát hình 9.4 để thực hiện các hoạt động.
Lời giải chi tiết:
- Các cặp góc bằng nhau của hai tam giác ABC và AMN: \(\widehat B = \widehat M{,^{}}\widehat C = \widehat N\)
- Có MN // BP, MB // NP (vì AB // NP) => MN=BP \( \Rightarrow \frac{{MN}}{{BC}} = \frac{{AN}}{{AC}} = \frac{{AM}}{{AB}}\)
- Có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\)=> ΔABC \(\backsim\) ΔAMN
Video hướng dẫn giải
Trong hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.
Phương pháp giải:
Quan sát hình 9.8 để kể tên các tam giác đồng dạng
Lời giải chi tiết:
ΔOCD \(\backsim\) ΔOAB
ΔOEF \(\backsim\) ΔODC
ΔOEF \(\backsim\) ΔOBA
Video hướng dẫn giải
Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Hãy giải thích bác Dương đã tính được chiều cao cột đèn như thế nào, biết cọc gỗ cao 1m, EC=80cm và EB=4m.
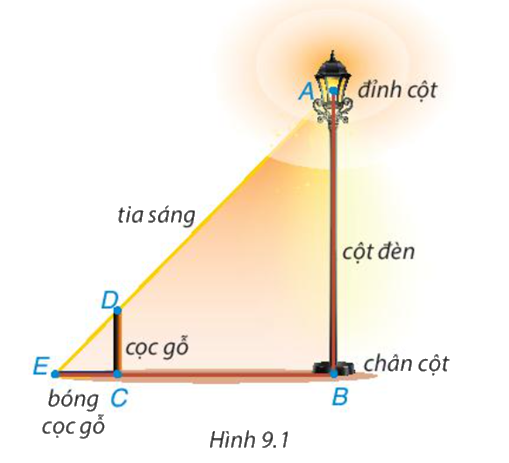
Phương pháp giải:
Dựa vào định lí ΔAEB \(\backsim\) ΔDEC và tìm tỉ số đồng dạng của chúng từ đó tính được chiều cao của cột đèn
Lời giải chi tiết:
Có EB=4m=400cm, CD=1m=100cm
Vì cọc gỗ và cột đèn đều thẳng đứng
=> AB // DC => ΔAEB \(\backsim\) ΔDEC \( \Rightarrow \frac{{DE}}{{A{\rm{E}}}} = \frac{{CE}}{{BE}} = \frac{{DC}}{{AB}}\)
Mà \(\frac{{CE}}{{A{\rm{E}}}} = \frac{{80}}{{100}} = \frac{1}{5}\)
=> Hai tam giác đồng dạng với tỉ số đồng dạng là \(\frac{1}{5}\)
\( \Rightarrow \frac{{DC}}{{AB}} = \frac{{100}}{{AB}} = \frac{1}{5}\)
=> AB=500cm=5m
Vậy cột đèn cao 5m
Mục 2 của chương trình Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về hình học, đặc biệt là các kiến thức liên quan đến tứ giác. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng suy luận.
Bài tập này yêu cầu học sinh nhắc lại các kiến thức cơ bản về tứ giác, bao gồm định nghĩa, các loại tứ giác đặc biệt (hình vuông, hình chữ nhật, hình thoi, hình bình hành, hình thang cân), các tính chất của tứ giác và các dấu hiệu nhận biết.
Bài tập này yêu cầu học sinh vận dụng các tính chất của tứ giác để giải các bài toán liên quan đến tính độ dài cạnh, số đo góc, chứng minh các tính chất hình học.
Ví dụ: Cho hình bình hành ABCD. Gọi E là giao điểm của hai đường chéo AC và BD. Chứng minh rằng AE = EC và BE = ED.
Lời giải:
Bài tập này yêu cầu học sinh áp dụng kiến thức về tứ giác để giải quyết các bài toán thực tế, ví dụ như tính chiều dài của một đoạn đường, tính góc của một hình ảnh, thiết kế một hình vẽ.
Ví dụ: Một mảnh đất hình chữ nhật có chiều dài 15m và chiều rộng 10m. Người ta muốn xây một con đường đi qua mảnh đất đó, con đường có dạng hình bình hành với chiều cao là 2m. Tính diện tích phần đất còn lại sau khi xây đường.
Lời giải:
Để giải các bài tập về tứ giác một cách hiệu quả, học sinh cần:
Trong quá trình giải bài tập, học sinh cần chú ý:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán 8 tập 2 - Kết nối tri thức. Chúc các em học tốt!