Bài 9.15 trang 92 SGK Toán 8 tập 2 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán. Bên cạnh đó, chúng tôi còn cung cấp các bài tập tương tự để học sinh tự luyện tập và củng cố kiến thức.
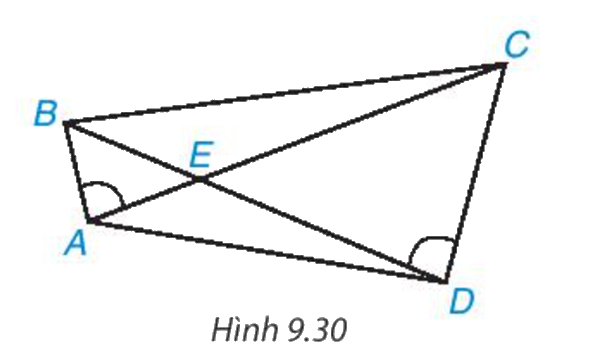
Cho các điểm A, B, C, D, E như Hình 9.30.
Đề bài
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat {BAC} = \widehat {C{\rm{D}}B}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Chứng minh\(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
- Chứng minh ΔAED ∽ ΔBEC (c.g.c)
Lời giải chi tiết
Xét hai tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {C{\rm{D}}B}\)(giả thiết)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra \(\Delta A{\rm{E}}B \backsim \Delta DEC\) (g.g) suy ra:
\(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Xét hai tam giác AED và BEC có:
\(\widehat {A{\rm{ED}}} = \widehat {BEC}\) (đối đỉnh)
\(\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Suy ra ΔAED ∽ ΔBEC (c.g.c)
Bài 9.15 SGK Toán 8 tập 2 Kết nối tri thức là một bài tập ứng dụng thực tế về hàm số bậc nhất. Để giải bài này, học sinh cần nắm vững các khái niệm về hàm số, cách xác định hàm số và cách biểu diễn hàm số trên mặt phẳng tọa độ.
Cho hàm số y = 2x + 3. Điểm nào sau đây thuộc đồ thị của hàm số?
Để kiểm tra một điểm thuộc đồ thị của hàm số y = 2x + 3, ta thay tọa độ x của điểm vào hàm số và tính giá trị y tương ứng. Nếu giá trị y tính được bằng với tung độ của điểm, thì điểm đó thuộc đồ thị của hàm số.
Vậy các điểm A(0; 3), C(-1; 1) và D(-2; -1) thuộc đồ thị của hàm số y = 2x + 3.
Ngoài bài 9.15, học sinh có thể gặp các dạng bài tập tương tự như:
Để giải tốt các bài tập về hàm số bậc nhất, học sinh cần:
Bài 9.15 trang 92 SGK Toán 8 tập 2 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, học sinh có thể tự tin giải bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.