Chào mừng bạn đến với bài học về Lý thuyết Hình chóp tứ giác đều trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình chóp tứ giác đều, giúp bạn tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau khám phá định nghĩa, các yếu tố của hình chóp tứ giác đều, tính chất và các ứng dụng thực tế của nó. Hãy bắt đầu ngay thôi!
Hình chóp tứ giác đều là gì?
1. Định nghĩa
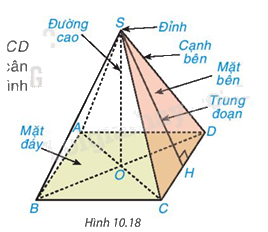
Hình chóp tứ giác đều có:
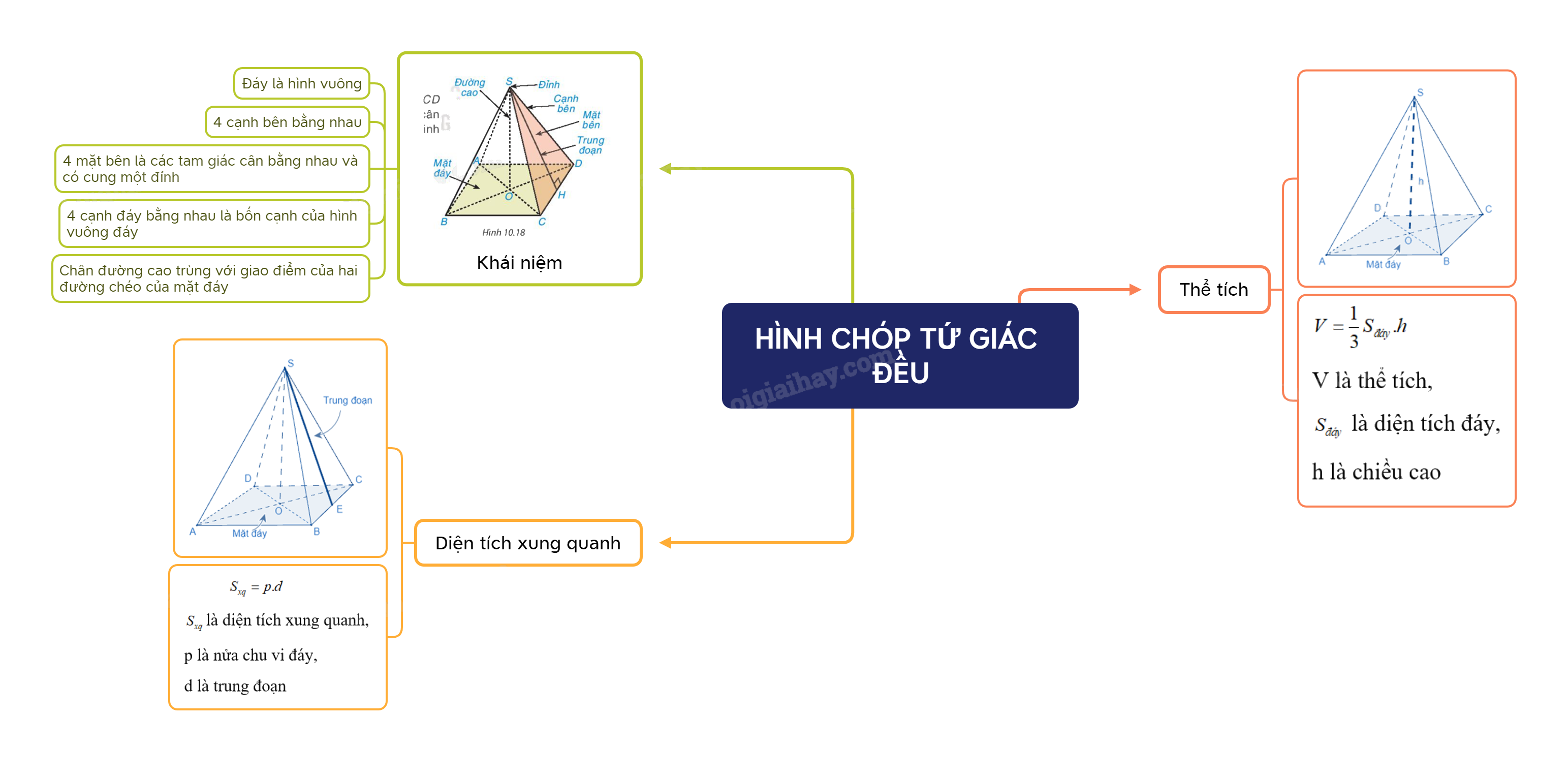
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao kẻ từ đỉnh tới mặt đáy là điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo)
2. Diện tích xung quanh và thể tích của hình chóp tứ giác đều
a. Diện tích xung quanh của hình chóp tứ giác đều
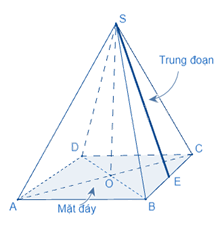
Diện tích xung quanh, kí hiệu là \({S_{xq}}\) của hình chóp tứ giác đều được tính theo công thức:
\({S_{xq}} = p.d\),
trong đó p là nửa chu vi đáy,
d là trung đoạn.
b. Thể tích của hình chóp tứ giác đều
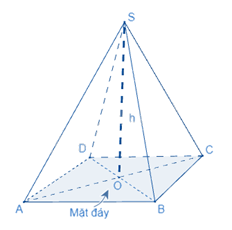
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(V = \frac{1}{3}S.h\)
trong đó V là thể tích,
S là diện tích đáy,
h là chiều cao.
Ví dụ: Cho hình chóp tứ giác đều sau:
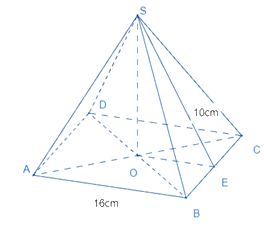
Diện tích xung quanh của hình chóp là: \({S_{xq}} = \frac{{16.4}}{2}.10 = 320(c{m^2})\)
Chiều cao của hình chóp là: \(SO = \sqrt {{{10}^2} - {{\left( {\frac{{16}}{2}} \right)}^2}} = 6(cm)\)
Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)
Hình chóp tứ giác đều là một trong những hình khối quan trọng trong chương trình Hình học lớp 8. Việc nắm vững lý thuyết về hình chóp tứ giác đều là nền tảng để giải quyết các bài toán liên quan đến tính diện tích, thể tích và các tính chất hình học khác.
Hình chóp tứ giác đều là hình chóp có đáy là một tứ giác đều và đỉnh của hình chóp nằm trên đường thẳng vuông góc với tâm của đáy.
Một hình chóp tứ giác đều được xác định bởi các yếu tố sau:
Hình chóp tứ giác đều có những tính chất quan trọng sau:
Diện tích xung quanh của hình chóp tứ giác đều được tính bằng công thức:
Sxq = p * d
Trong đó:
Diện tích toàn phần của hình chóp tứ giác đều được tính bằng công thức:
Stp = Sxq + Sđáy
Trong đó:
Thể tích của hình chóp tứ giác đều được tính bằng công thức:
V = (1/3) * Sđáy * h
Trong đó:
Để hiểu rõ hơn về lý thuyết hình chóp tứ giác đều, bạn có thể thực hành giải các bài tập sau:
Hy vọng rằng bài học về Lý thuyết Hình chóp tứ giác đều SGK Toán 8 - Kết nối tri thức này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập liên quan.