Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 2 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 12 trang 136, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán. Hãy cùng bắt đầu với bài 12 trang 136 nhé!
Cho tam giác ABC không phải là tam giác vuông,
Đề bài
Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ΔABE \(\backsim\) ΔACF , từ đó suy ra ΔAEF \(\backsim\) ΔABC
b) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\) ΔACF
b) Sử dụng các tỉ số đồng dạng của hai tam giác để tính EF
Lời giải chi tiết
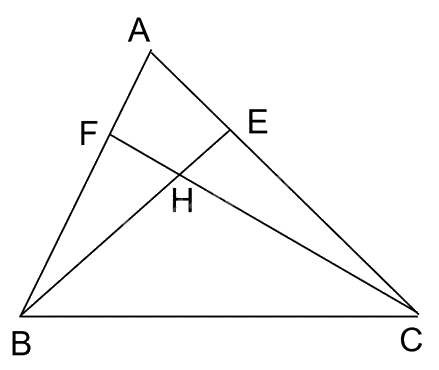
a) Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung => ΔABE \(\backsim\) ΔACF
=> \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)
Xét tam giác AEF và tam giác ABC có: A chung và \(\frac{{AB}}{{AC}} = \frac{{A{\rm{E}}}}{{AF}}\)
=> ΔAEF \(\backsim\) ΔABC (c.g.c)
b) Xét tam giác vuông AEB có
=> \(A{{\rm{E}}^2} = A{B^2} - B{E^2}\)
=> \(A{{\rm{E}}^2} = {10^2} - {8^2}\)
=> AE=6 cm
Vì ΔAEF \(\backsim\) ΔABC
=> \(\frac{{A{\rm{E}}}}{{AB}} = \frac{{EF}}{{BC}}\)
=> \(\frac{6}{{10}} = \frac{{EF}}{{15}}\)
=> EF=9 cm
Bài 12 trang 136 SGK Toán 8 tập 2 - Kết nối tri thức thuộc chương trình học về các tứ giác đặc biệt, cụ thể là hình thang cân. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức lý thuyết cơ bản về hình thang cân, bao gồm:
Bài 12 yêu cầu chúng ta chứng minh một tứ giác là hình thang cân dựa trên các điều kiện cho trước. Để làm được điều này, chúng ta cần áp dụng các dấu hiệu nhận biết hình thang cân đã học. Dưới đây là hướng dẫn giải chi tiết:
Để chứng minh ABCD là hình thang cân, chúng ta cần chứng minh AB song song CD và AD = BC. Thông thường, đề bài sẽ cung cấp các thông tin về góc hoặc độ dài cạnh để chúng ta suy luận. Ví dụ, nếu đề bài cho góc DAB = góc ABC, thì chúng ta có thể kết luận AB song song CD (vì có hai góc trong cùng phía bù nhau). Sau đó, nếu đề bài cho AD = BC, thì chúng ta có thể kết luận ABCD là hình thang cân.
Sau khi chứng minh được ABCD là hình thang cân, chúng ta có thể tính độ dài các cạnh và đường cao của hình thang. Để tính độ dài các cạnh, chúng ta có thể sử dụng định lý Pitago trong các tam giác vuông được tạo thành khi kẻ đường cao từ đỉnh của đáy lớn xuống đáy nhỏ. Để tính đường cao, chúng ta có thể sử dụng công thức tính diện tích hình thang hoặc các mối quan hệ giữa các cạnh và góc trong hình thang cân.
Giả sử đề bài cho hình thang ABCD có AB song song CD, AD = BC = 5cm, và góc DAB = 60 độ. Hãy tính độ dài các cạnh CD và đường cao AH của hình thang.
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong SGK Toán 8 tập 2 - Kết nối tri thức và các tài liệu tham khảo khác. Hãy chú trọng việc hiểu rõ lý thuyết và áp dụng linh hoạt các dấu hiệu nhận biết và tính chất của hình thang cân để giải quyết các bài toán một cách hiệu quả.
Bài 12 trang 136 SGK Toán 8 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp bạn hiểu sâu hơn về hình thang cân. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.