Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 54, 55 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em tự tin hơn trong quá trình học tập và ôn luyện môn Toán.
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau: - Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B. - Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau. b) Hình thang ABCD có là hình thang cân không? Vì sao?
Video hướng dẫn giải
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
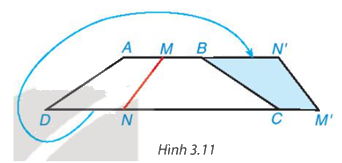
Phương pháp giải:
Quan sát hình 3.11 chứng minh MN’M’N là hình thang có\(\widehat N = \widehat {M'}\) nên tứ giác MN”M”N là hình thang cân.
Lời giải chi tiết:
Ta cắt một mảnh giấy hình thang cân ABCD bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật hình thang AMND rồi ghép với hình thang MBCN dọc theo các cạnh bên của hình thang ban đầu, khi đó ta được một hình mới.
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Vì AB // CD nên \(\widehat {AMN} = \widehat {MNC}\) (2 góc so le trong)
Mà \(\widehat {AMN} = \widehat {CM'N'}\)(theo giả thiết)
\( \Rightarrow \widehat {MNC} = \widehat {CM'N}\)
Mà hai góc này là hai góc kề một đáy nên suy ra MN’M’N là hình thang cân.
Video hướng dẫn giải
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
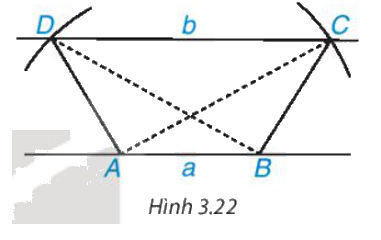
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Phương pháp giải:
Hình thang ABCD có hai đường chéo AC = BD.
Do đó ABCD là hình thang cân.
Lời giải chi tiết:
a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.
b) Hình thang ABCD có hai đường chéo AC = BD.
Do đó ABCD là hình thang cân.
Video hướng dẫn giải
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
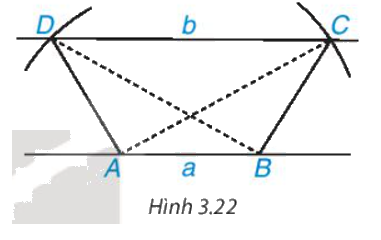
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Phương pháp giải:
Hình thang ABCD có hai đường chéo AC = BD.
Do đó ABCD là hình thang cân.
Lời giải chi tiết:
a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.
b) Hình thang ABCD có hai đường chéo AC = BD.
Do đó ABCD là hình thang cân.
Video hướng dẫn giải
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
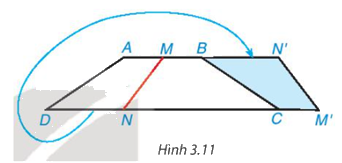
Phương pháp giải:
Quan sát hình 3.11 chứng minh MN’M’N là hình thang có\(\widehat N = \widehat {M'}\) nên tứ giác MN”M”N là hình thang cân.
Lời giải chi tiết:
Ta cắt một mảnh giấy hình thang cân ABCD bằng một nhát thẳng cắt cả hai cạnh đáy.
Lật hình thang AMND rồi ghép với hình thang MBCN dọc theo các cạnh bên của hình thang ban đầu, khi đó ta được một hình mới.
Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.
Do đó MN’M’N là hình thang.
Vì AB // CD nên \(\widehat {AMN} = \widehat {MNC}\) (2 góc so le trong)
Mà \(\widehat {AMN} = \widehat {CM'N'}\)(theo giả thiết)
\( \Rightarrow \widehat {MNC} = \widehat {CM'N}\)
Mà hai góc này là hai góc kề một đáy nên suy ra MN’M’N là hình thang cân.
Mục 3 trang 54, 55 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Đây là một phần quan trọng trong chương trình học, giúp học sinh nắm vững nền tảng để giải quyết các bài toán phức tạp hơn ở các chương sau.
(a) (3x + 2y) + (2x - y)
Giải: (3x + 2y) + (2x - y) = 3x + 2y + 2x - y = (3x + 2x) + (2y - y) = 5x + y
(b) (5x2 - 3x + 2) - (2x2 + x - 1)
Giải: (5x2 - 3x + 2) - (2x2 + x - 1) = 5x2 - 3x + 2 - 2x2 - x + 1 = (5x2 - 2x2) + (-3x - x) + (2 + 1) = 3x2 - 4x + 3
(a) x2 - 4
Giải: x2 - 4 = (x - 2)(x + 2) (Sử dụng hằng đẳng thức hiệu hai bình phương)
(b) x3 + 8
Giải: x3 + 8 = (x + 2)(x2 - 2x + 4) (Sử dụng hằng đẳng thức tổng hai lập phương)
(x + y)2 = x2 + 2xy + y2
Giải: (x + y)2 = (x + y)(x + y) = x(x + y) + y(x + y) = x2 + xy + yx + y2 = x2 + 2xy + y2
Khi thực hiện các phép toán với đa thức, cần chú ý đến các quy tắc về dấu và bậc của đa thức. Khi phân tích đa thức thành nhân tử, cần tìm các nhân tử chung và áp dụng các hằng đẳng thức một cách linh hoạt. Khi chứng minh đẳng thức, cần biến đổi một vế về dạng tương đương với vế còn lại.
Hy vọng bài giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về Mục 3 trang 54, 55 SGK Toán 8 tập 1 - Kết nối tri thức và tự tin hơn trong quá trình học tập. Chúc các em học tốt!