Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 119 sách giáo khoa Toán 8 tập 2 - Kết nối tri thức.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, rõ ràng và dễ tiếp thu nhất.
Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều
Video hướng dẫn giải
Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 2m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều
Lời giải chi tiết:
Nửa chu vi đáy của chiếc hộp gỗ là: (4.2):2=4 (m)
Diện tích xung quanh của chiếc hộp gỗ là: \(S_{xq}=p.d=3.4=12 (m^2)\)
Chi phí bác Khôi phải trả là: 30000.12=360000 (đồng)
Video hướng dẫn giải
Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công Nguyên là một trong những công trình cố nhất và duy nhất còn tồn tại trong số bảy kì quan thế giới cố đại. Kim tự tháp này có dạng hình chóp tứ giác đều cao 147m, cạnh đáy dài 230m (H10.17). Kim tự tháp Kheops có thể tích bằng bao nhiêu?

Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều
Lời giải chi tiết:
Vì kim tự tháp Kheops có hình chóp tứ giác đều nên thể tích của kim tự tháp Kheops là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.230.230.147 = {2^{}}{592^{}}100\left( {{m^3}} \right)\)
Video hướng dẫn giải
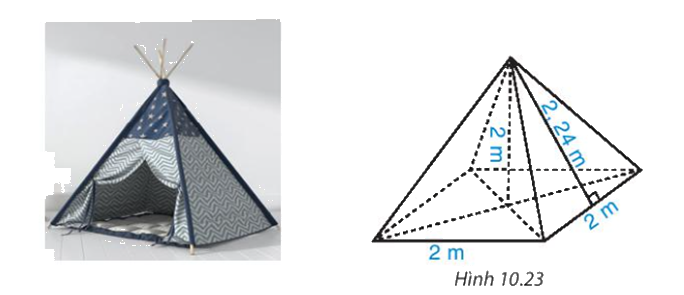
Một chiếc lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 2 m, chiều cao bằng 2 m
a) Thể tích không khí trong lều là bao nhiêu?
b) Biết lều phủ vải bốn phía và cả mặt tiếp đất. Tính diện tích vải bạt cần dùng (coi mép nối không đáng kể), biết rằng người ta đo chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m.
Phương pháp giải:
- Tính thể tích không khí trong lều bằng công thức tính thể tích của hình chóp tứ giác đều.
- Diện tích bạt vải cần dùng là: Sxq + Sđ
Lời giải chi tiết:
a) Có diện tích đáy lều là: 2.2=4 (m2)
Thể tích không khí trong lều là: \(V = \frac{1}{3}.S.h = \frac{1}{3}.4.2 = \frac{8}{3}\left( {{m^3}} \right)\)
b) Nửa chu vi đáy lều là: (2.4):2=4 (m)
- Có \({S_{xq}} = p.d = 4.2,24 = 8,96({m^2})\)
=> Diện tích bạt vải cần dùng là: Sxq + Sđ = 8,96 + 4 = 12,96 (m2)
Video hướng dẫn giải
Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 2m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều
Lời giải chi tiết:
Nửa chu vi đáy của chiếc hộp gỗ là: (4.2):2=4 (m)
Diện tích xung quanh của chiếc hộp gỗ là: \(S_{xq}=p.d=3.4=12 (m^2)\)
Chi phí bác Khôi phải trả là: 30000.12=360000 (đồng)
Video hướng dẫn giải
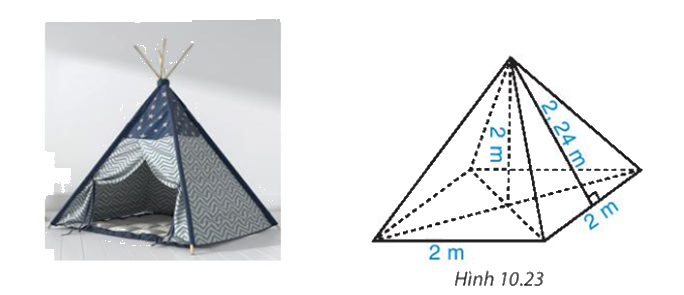
Một chiếc lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 2 m, chiều cao bằng 2 m
a) Thể tích không khí trong lều là bao nhiêu?
b) Biết lều phủ vải bốn phía và cả mặt tiếp đất. Tính diện tích vải bạt cần dùng (coi mép nối không đáng kể), biết rằng người ta đo chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m.
Phương pháp giải:
- Tính thể tích không khí trong lều bằng công thức tính thể tích của hình chóp tứ giác đều.
- Diện tích bạt vải cần dùng là: Sxq + Sđ
Lời giải chi tiết:
a) Có diện tích đáy lều là: 2.2=4 (m2)
Thể tích không khí trong lều là: \(V = \frac{1}{3}.S.h = \frac{1}{3}.4.2 = \frac{8}{3}\left( {{m^3}} \right)\)
b) Nửa chu vi đáy lều là: (2.4):2=4 (m)
- Có \({S_{xq}} = p.d = 4.2,24 = 8,96({m^2})\)
=> Diện tích bạt vải cần dùng là: Sxq + Sđ = 8,96 + 4 = 12,96 (m2)
Video hướng dẫn giải
Kim tự tháp Kheops ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công Nguyên là một trong những công trình cố nhất và duy nhất còn tồn tại trong số bảy kì quan thế giới cố đại. Kim tự tháp này có dạng hình chóp tứ giác đều cao 147m, cạnh đáy dài 230m (H10.17). Kim tự tháp Kheops có thể tích bằng bao nhiêu?

Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều
Lời giải chi tiết:
Vì kim tự tháp Kheops có hình chóp tứ giác đều nên thể tích của kim tự tháp Kheops là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.230.230.147 = {2^{}}{592^{}}100\left( {{m^3}} \right)\)
Mục 2 trang 119 SGK Toán 8 tập 2 - Kết nối tri thức thường tập trung vào việc vận dụng các kiến thức đã học về hình học, cụ thể là các định lý liên quan đến tứ giác, đường trung bình của tam giác, và các tính chất của hình thang cân. Các bài tập trong mục này thường yêu cầu học sinh chứng minh các tính chất, tính toán độ dài đoạn thẳng, góc, và giải quyết các bài toán thực tế liên quan đến hình học.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2 trang 119, chúng ta sẽ đi vào phân tích chi tiết từng bài tập:
Bài 1 thường yêu cầu học sinh vận dụng kiến thức về đường trung bình của tam giác để chứng minh một đoạn thẳng song song với một cạnh của tam giác. Để giải bài này, học sinh cần nắm vững định nghĩa và tính chất của đường trung bình của tam giác. Ví dụ, nếu M là trung điểm của AB và N là trung điểm của AC thì MN là đường trung bình của tam giác ABC và MN song song với BC.
Bài 2 có thể yêu cầu học sinh tính độ dài một đoạn thẳng trong hình thang cân. Để giải bài này, học sinh cần sử dụng các tính chất của hình thang cân, chẳng hạn như hai cạnh bên bằng nhau, hai góc kề một cạnh bên bằng nhau, và đường trung bình của hình thang cân bằng trung bình cộng của hai đáy. Ngoài ra, học sinh cũng có thể cần sử dụng định lý Pitago để tính độ dài các đoạn thẳng trong tam giác vuông.
Bài 3 thường là một bài toán thực tế liên quan đến hình học, yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết vấn đề. Ví dụ, bài toán có thể yêu cầu tính chiều cao của một ngọn núi dựa trên số liệu đo đạc được từ mặt đất. Để giải bài này, học sinh cần phân tích bài toán, vẽ hình minh họa, và sử dụng các công thức và định lý phù hợp.
Để giải các bài tập hình học một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
Khi giải bài tập hình học, học sinh cần lưu ý những điều sau:
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hình học hiệu quả, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 119 SGK Toán 8 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!