Chào mừng bạn đến với bài học về Lý thuyết Ba trường hợp đồng dạng của hai tam giác trong chương trình Toán 8 - Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đồng dạng tam giác, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu về điều kiện để hai tam giác đồng dạng, các trường hợp đồng dạng và ứng dụng của lý thuyết này trong việc giải toán.
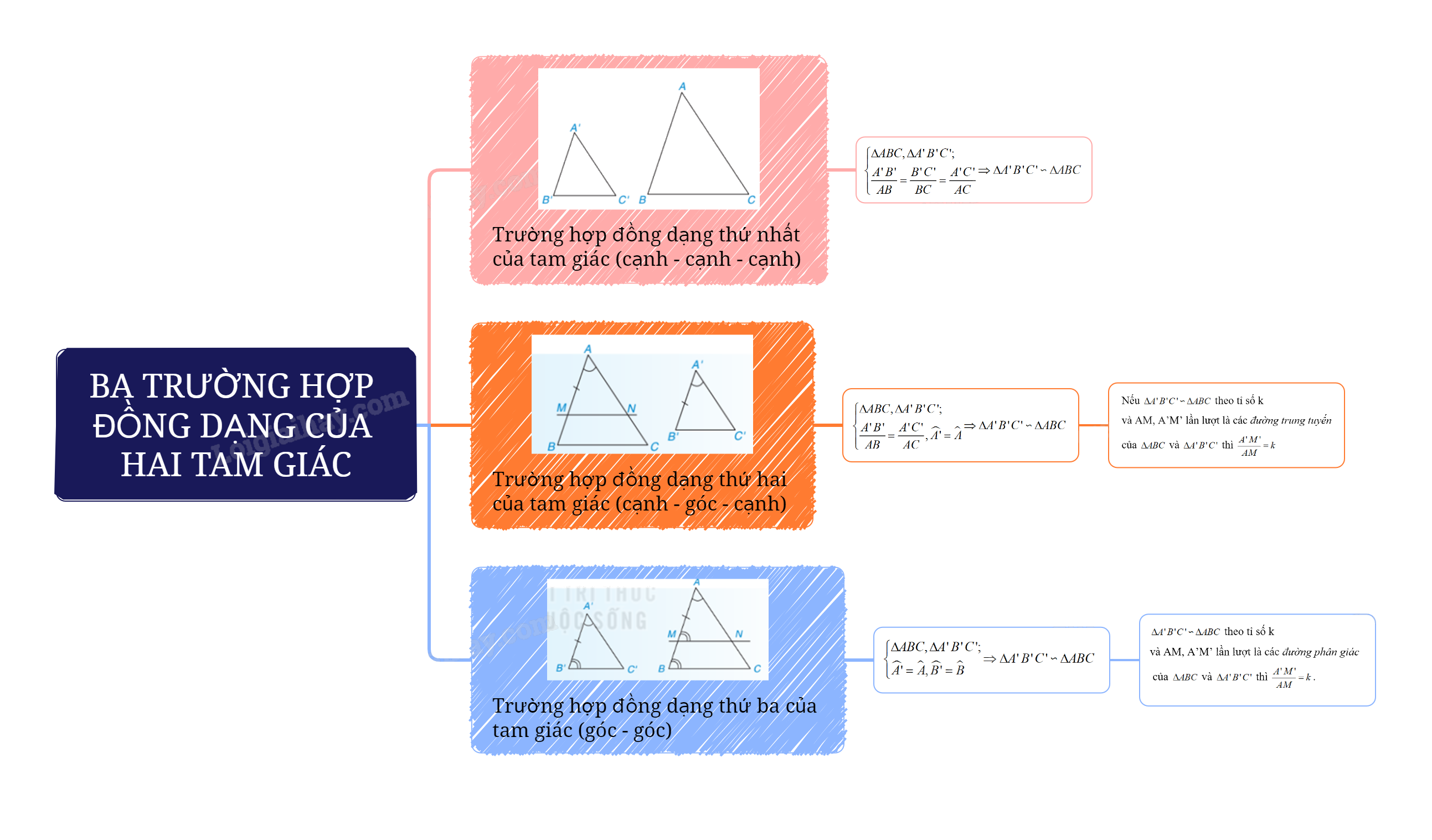
Ba trường hợp đồng dạng của hai tam giác là gì?
1. Trường hợp đồng dạng thứ nhất của tam giác
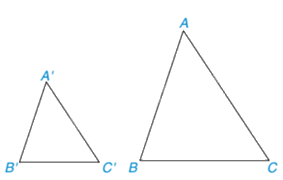
Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
2. Trường hợp đồng dạng thứ hai của tam giác
Trường hợp đồng dạng cạnh – góc – cạnh:
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
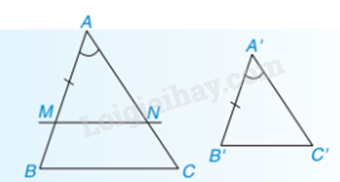
Nhận xét: Nếu \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số k và AM, A’M’ lần lượt là các đường trung tuyến của \(\Delta ABC\) và \(\Delta A'B'C'\) thì \(\frac{{A'M'}}{{AM}} = k\)
3. Trường hợp đồng dạng thứ ba của tam giác
Trường hợp đồng dạng góc – góc:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
\(\left\{ \begin{array}{l}\Delta ABC,\Delta A'B'C';\\\widehat {A'} = \widehat A,\widehat {B'} = \widehat B\end{array} \right. \Rightarrow \Delta A'B'C' \backsim \Delta ABC\)
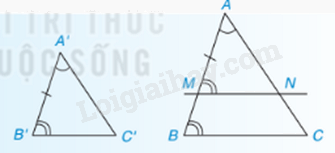
Nhận xét: \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số k và AM, A’M’ lần lượt là các đường phân giác của \(\Delta ABC\) và \(\Delta A'B'C'\) thì \(\frac{{A'M'}}{{AM}} = k\)
Trong chương trình Toán 8, phần hình học đóng vai trò quan trọng trong việc phát triển tư duy logic và khả năng giải quyết vấn đề. Một trong những kiến thức nền tảng của chương này là Lý thuyết Ba trường hợp đồng dạng của hai tam giác. Bài viết này sẽ trình bày chi tiết lý thuyết này, kèm theo các ví dụ minh họa và bài tập vận dụng để giúp bạn hiểu rõ hơn.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C'
Điều kiện cần và đủ để ΔABC ~ ΔA'B'C' là:
Có ba trường hợp đồng dạng của hai tam giác thường được sử dụng:
ΔABC ~ ΔA'B'C' nếu ∠A = ∠A' và ∠B = ∠B' (hoặc ∠A = ∠A' và ∠C = ∠C', hoặc ∠B = ∠B' và ∠C = ∠C').
Ví dụ: Cho ΔABC có ∠A = 60°, ∠B = 80°. Cho ΔA'B'C' có ∠A' = 60°, ∠B' = 80°. Chứng minh ΔABC ~ ΔA'B'C'.
ΔABC ~ ΔA'B'C' nếu AB/A'B' = AC/A'C' và ∠A = ∠A'.
Ví dụ: Cho ΔABC có AB = 5cm, AC = 7cm, ∠A = 40°. Cho ΔA'B'C' có A'B' = 10cm, A'C' = 14cm, ∠A' = 40°. Chứng minh ΔABC ~ ΔA'B'C'.
ΔABC ~ ΔA'B'C' nếu AB/A'B' = BC/B'C' = CA/C'A'.
Ví dụ: Cho ΔABC có AB = 3cm, BC = 4cm, CA = 5cm. Cho ΔA'B'C' có A'B' = 6cm, B'C' = 8cm, C'A' = 10cm. Chứng minh ΔABC ~ ΔA'B'C'.
Lý thuyết đồng dạng tam giác có nhiều ứng dụng trong thực tế và trong các bài toán hình học khác. Một số ứng dụng tiêu biểu:
Bài 1: Cho ΔABC vuông tại A, có AB = 3cm, AC = 4cm. Gọi D là điểm sao cho ΔABC ~ ΔDBA. Tính độ dài AD.
Bài 2: Cho ΔABC có AB = 6cm, BC = 8cm, CA = 10cm. Gọi M là trung điểm của AB, N là trung điểm của AC. Chứng minh ΔAMN ~ ΔABC.
Lý thuyết Ba trường hợp đồng dạng của hai tam giác là một kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.