Chào mừng bạn đến với chuyên mục lý thuyết Giải bài toán bằng cách lập phương trình của chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng giúp học sinh rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Chúng tôi cung cấp lý thuyết đầy đủ, dễ hiểu, kèm theo các ví dụ minh họa chi tiết, giúp bạn nắm vững kiến thức nền tảng và tự tin áp dụng vào giải các bài tập thực tế.
Giải bài toán bằng cách lập phương trình như thế nào?
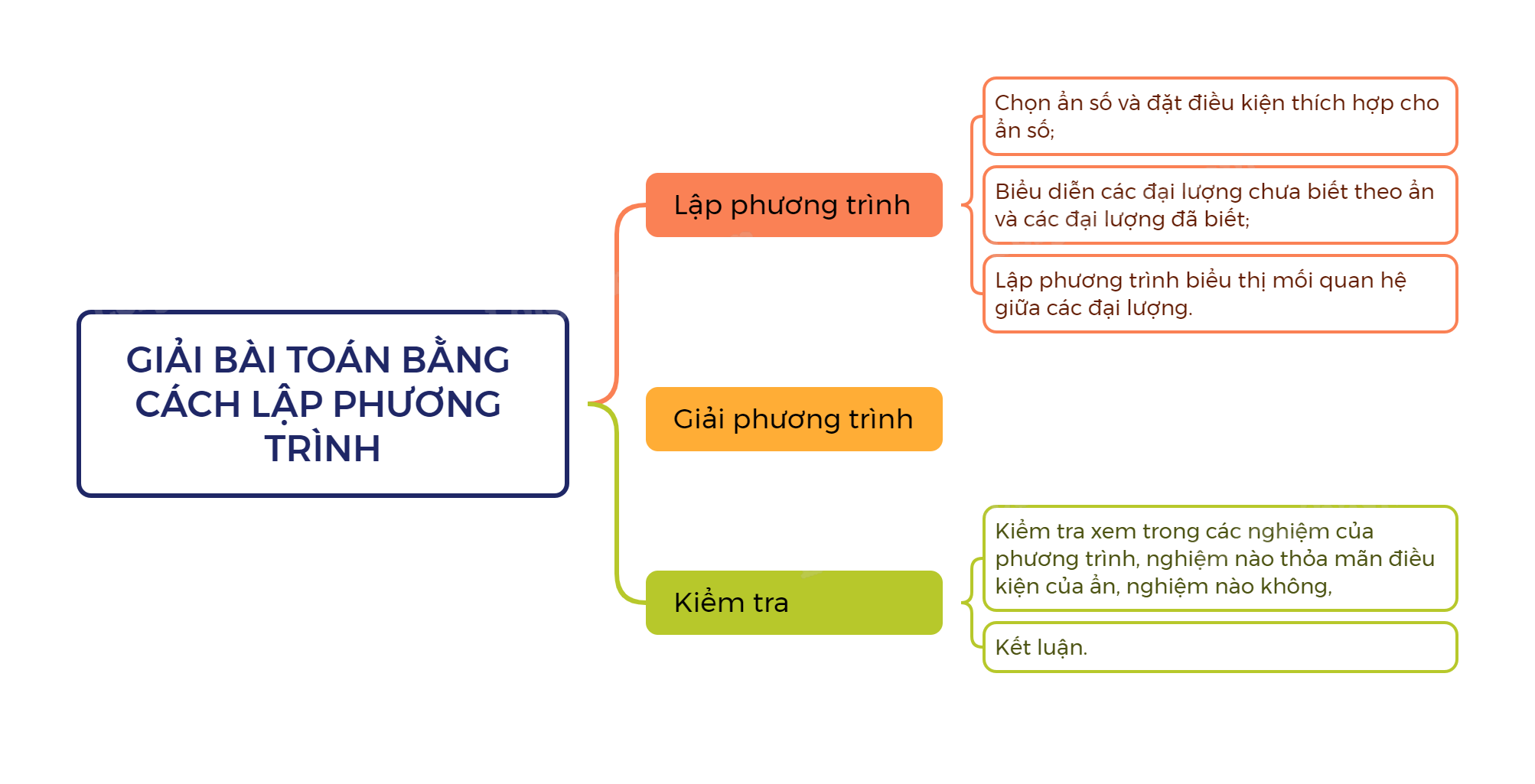
Các bước giải bài toán bằng cách lập phương trình:
Bước 1. Lập phương trình:
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số;
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Giải bài toán bằng cách lập phương trình là một phương pháp quan trọng trong toán học, đặc biệt là ở cấp trung học cơ sở. Phương pháp này giúp chuyển đổi các bài toán thực tế thành các bài toán đại số, từ đó dễ dàng giải quyết bằng các công cụ toán học quen thuộc.
Phương trình là một đẳng thức chứa ẩn. Ẩn là một đại lượng chưa biết, thường được ký hiệu bằng các chữ cái như x, y, z,... Việc giải phương trình là tìm giá trị của ẩn để đẳng thức trở thành đúng.
Ví dụ 1: Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau 30 phút, một người khác đi xe máy từ B đến A với vận tốc 50km/h. Biết quãng đường AB dài 100km. Hỏi sau bao lâu kể từ khi người thứ nhất xuất phát thì hai người gặp nhau?
Giải:
Phương trình: 40x + 50(x - 0.5) = 100
Giải phương trình, ta được x = 1.14 (giờ)
Vậy sau 1.14 giờ kể từ khi người thứ nhất xuất phát thì hai người gặp nhau.
Ví dụ 2: Một lớp có 35 học sinh. Số học sinh nam nhiều hơn số học sinh nữ là 3 em. Tính số học sinh nam và số học sinh nữ của lớp.
Giải:
Phương trình: x - (35 - x) = 3
Giải phương trình, ta được x = 19
Vậy số học sinh nam của lớp là 19 em và số học sinh nữ của lớp là 16 em.
Để nắm vững kiến thức về giải bài toán bằng cách lập phương trình, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng và tự tin giải quyết các bài toán phức tạp.
Lý thuyết Giải bài toán bằng cách lập phương trình là một công cụ hữu ích trong toán học. Việc nắm vững các bước giải bài toán và luyện tập thường xuyên sẽ giúp bạn thành thạo phương pháp này và đạt kết quả tốt trong học tập.