Chào mừng bạn đến với bài học lý thuyết Phân thức đại số thuộc chương trình Toán 8 - Kết nối tri thức. Bài viết này sẽ cung cấp kiến thức nền tảng, định nghĩa, tính chất và các ví dụ minh họa giúp bạn hiểu rõ về phân thức đại số.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và phương pháp giải bài tập hiệu quả.
Phân thức đại số là gì?
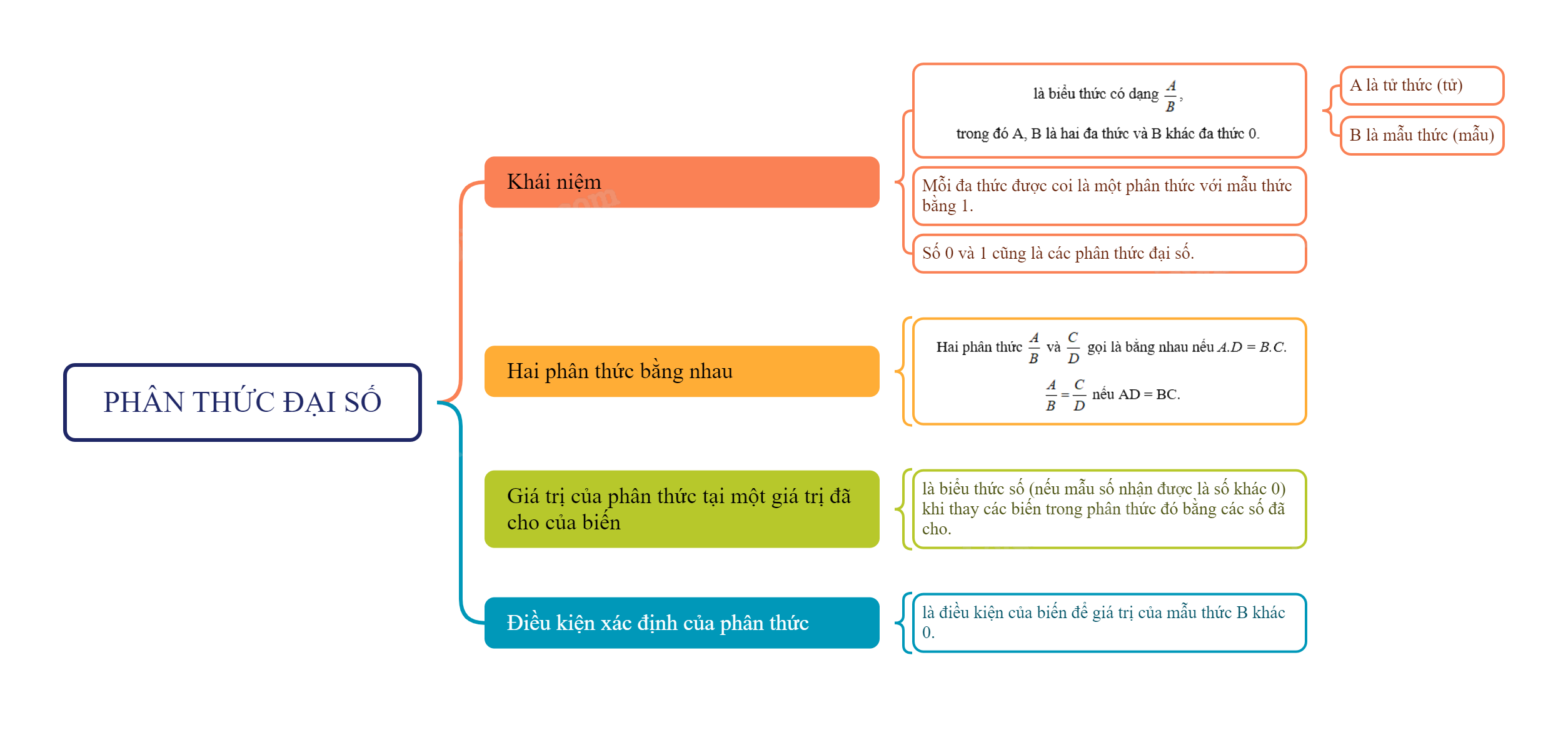
1. Phân thức đại số
Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng \(\frac{A}{B}\), trong đó A, B là hai đa thức và B khác đa thức 0.
A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).
Nhận xét. Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1.
Số 0 và số 1 cũng là các phân thức đại số
Ví dụ:
\(\frac{{2x + 1}}{{x - 3}};\frac{{ab}}{{a + b}};{x^2} + 3x + 2;\sqrt 2 \) là các phân thức đại số.
\(\sqrt x ;\sqrt[3]{x}\) không phải là phân thức vì \(\sqrt x ;\sqrt[3]{x}\) không phải là đa thức.
2. Hai phân thức bằng nhau
Hai phân thức \(\frac{A}{B}\) và \(\frac{C}{D}\) gọi làbằng nhau nếu A.D = B.C.
\(\frac{A}{B} = \frac{C}{D}\) nếu AD = BC.
Ví dụ: Hai phân thức \(\frac{{x{y^2}}}{{xy + y}}\) và \(\frac{{xy}}{{x + 1}}\) bằng nhau vì \(x{y^2}.(x + 1) = xy(xy + y)\)
3. Giá trị của phân thức tại một giá trị đã cho của biến
Giá trị của phân thức tại các giá trị đã cho của biến là biểu thức số (nếu mẫu số nhận được là số khác 0) khi thay các biến trong phân thức đó bằng các số đã cho.
Để tính giá trị của phân thức tại những giá trị cho trước của biến, ta thay các giá trị cho trước của biến vào phân thức đó rồi tính giá trị của biểu thức số nhận được.
4. Điều kiện xác định của phân thức
Điều kiện xác định của phân thức \(\frac{A}{B}\) là điều kiện của biến để giá trị của mẫu thức B khác 0.
Ví dụ: Phân thức P = \(\frac{{x + 3}}{{x - 1}}\) xác định khi \(x - 1 \ne 0\) hay \(x \ne 1\)
Tại x = 3, \(P = \frac{{3 + 3}}{{3 - 1}} = \frac{6}{2} = 3\)
Phân thức đại số là một khái niệm quan trọng trong đại số, đặc biệt là ở chương trình Toán 8. Việc nắm vững lý thuyết về phân thức đại số là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ trình bày chi tiết lý thuyết phân thức đại số theo chương trình SGK Toán 8 - Kết nối tri thức.
Một phân thức đại số là biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. P được gọi là tử thức, Q được gọi là mẫu thức.
Ví dụ:
Phân thức P/Q chỉ xác định khi và chỉ khi mẫu thức Q khác 0. Điều này có nghĩa là chúng ta cần tìm các giá trị của biến x sao cho Q ≠ 0.
Ví dụ:
Phân thức x + 1 / x - 2 xác định khi x - 2 ≠ 0, tức là x ≠ 2.
Giống như các phân số thông thường, phân thức đại số cũng có các tính chất cơ bản sau:
Rút gọn phân thức đại số là việc biến đổi phân thức thành một phân thức đơn giản hơn, có tử thức và mẫu thức không có nhân tử chung.
Để rút gọn phân thức, ta thực hiện các bước sau:
Ví dụ:
Rút gọn phân thức (x2 - 1) / (x + 1):
Vậy, phân thức (x2 - 1) / (x + 1) được rút gọn thành x - 1.
Quy đồng mẫu thức là việc biến đổi các phân thức có mẫu thức khác nhau thành các phân thức có cùng mẫu thức. Để quy đồng mẫu thức, ta thực hiện các bước sau:
Ví dụ:
Quy đồng mẫu thức của các phân thức 1/x và 1/(x + 1):
Các phép toán cộng, trừ, nhân, chia phân thức đại số được thực hiện tương tự như các phép toán trên phân số thông thường, nhưng cần chú ý đến điều kiện xác định của phân thức.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Phân thức đại số SGK Toán 8 - Kết nối tri thức. Chúc bạn học tập tốt!