Bài 9.22 trang 97 SGK Toán 8 tập 2 thuộc chương 4: Các hình song song – Hình thang của sách Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về tính chất của hình thang cân để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán. Bên cạnh đó, chúng tôi còn cung cấp các bài tập tương tự để học sinh tự luyện tập và củng cố kiến thức.
Chú cún bị xích bởi một sợi dây dài 6m để canh
Đề bài
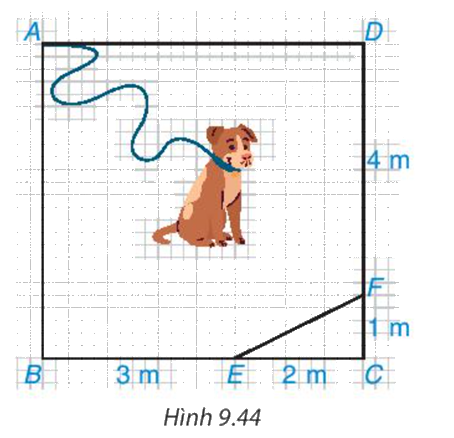
Chú cún bị xích bởi một sợi dây dài 6m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5m như Hình 9.44. Đầu xích buộc cố định tại điểm A của mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore trong tam giác vuông
Lời giải chi tiết
- Xét tam giác ABE vuông tại B, có
\(A{{\rm{E}}^2} = A{B^2} + B{E^2} = {5^2} + {3^2} = 34 \Rightarrow A{\rm{E}} = \sqrt {34} cm\)
=> Chú chó có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây
- Xét tam giác ADF vuông tại D, có
\({\rm{A}}{{\rm{F}}^2} = A{{\rm{D}}^2} + D{F^2} = {5^2} + {4^2} = 41 \Rightarrow A{\rm{F}} = \sqrt {41} cm\)
=> Chú chó không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây
- Xét tam giác ADC vuông tại D, có
\(A{C^2} = A{{\rm{D}}^2} + D{C^2} = {5^2} + {5^2} = 50 \Rightarrow A{\rm{C}} = 5\sqrt 2 cm\)
=> Chú chó không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây
Vậy chú chó không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E
Bài 9.22 trang 97 SGK Toán 8 tập 2 yêu cầu chúng ta giải quyết một bài toán liên quan đến hình thang cân. Để giải bài toán này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), có AB = 5cm, CD = 10cm, AD = 6cm. Tính chiều cao của hình thang.)
Lời giải:
Kết luận: Chiều cao của hình thang ABCD là khoảng 5.45cm.
Ngoài bài toán trên, còn rất nhiều dạng bài tập liên quan đến hình thang cân mà học sinh có thể gặp phải. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để giải các bài tập này một cách hiệu quả, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, học sinh có thể tự giải các bài tập sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh sẽ hiểu rõ hơn về bài 9.22 trang 97 SGK Toán 8 tập 2 - Kết nối tri thức và tự tin giải quyết các bài toán tương tự.
Việc học toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết và làm bài tập để nắm vững kiến thức và đạt kết quả tốt nhất.