Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 65, 66 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những nội dung chất lượng, chính xác và cập nhật nhất để hỗ trợ các em trong quá trình học tập. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Video hướng dẫn giải
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Phương pháp giải:
Sử dụng định lí tổng ba góc của một tứ giác.
Lời giải chi tiết:

Vì ABCD là hình bình hành nên \(\widehat A = \widehat C;\widehat B = \widehat D\)
Suy ra \(\widehat A = \widehat C = {90^o}\)
Ta có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
90°+\(\widehat B\)+90°+\(\widehat B\)=360°
2\(\widehat B\)+180°=360°
Suy ra 2\(\widehat B\)=360°−180°=180°
Mà \(\widehat B = \widehat D\) nên \(\widehat B = \widehat D = {90^o}\)
Do đó \(\widehat B = \widehat C = \widehat D = {90^o}\)
Hình bình hành ABCD là hình chữ nhật vì \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Video hướng dẫn giải
Cho tứ giác ABCD có \(\widehat A = {90^o}\), hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
Phương pháp giải:
Chứng minh tứ giác ABCD là hình bình hành có \(\widehat A = {90^o}\)nên ABCD là hình chữ nhật
Lời giải chi tiết:

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên tứ giác ABCD là hình bình hành.
Hình bình hành ABCD là có \(\widehat A = {90^o}\)
Do đó, tứ giác ABCD là hình chữ nhật.
Video hướng dẫn giải
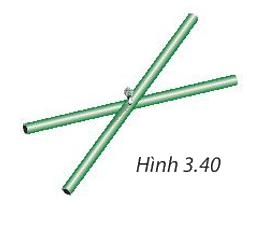
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
Phương pháp giải:
Nhận xét về hai thanh tre tạo thành hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
Video hướng dẫn giải
Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D. Tứ giác ABCD có là hình chữ nhật không? Vì sao?
Phương pháp giải:
Sử dụng định lí tổng ba góc của một tứ giác.
Lời giải chi tiết:

Vì ABCD là hình bình hành nên \(\widehat A = \widehat C;\widehat B = \widehat D\)
Suy ra \(\widehat A = \widehat C = {90^o}\)
Ta có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
90°+\(\widehat B\)+90°+\(\widehat B\)=360°
2\(\widehat B\)+180°=360°
Suy ra 2\(\widehat B\)=360°−180°=180°
Mà \(\widehat B = \widehat D\) nên \(\widehat B = \widehat D = {90^o}\)
Do đó \(\widehat B = \widehat C = \widehat D = {90^o}\)
Hình bình hành ABCD là hình chữ nhật vì \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Video hướng dẫn giải
Cho tứ giác ABCD có \(\widehat A = {90^o}\), hai đường chéo cắt nhau tại trung điểm O của mỗi đường. Hỏi tứ giác ABCD là hình gì? Tại sao?
Phương pháp giải:
Chứng minh tứ giác ABCD là hình bình hành có \(\widehat A = {90^o}\)nên ABCD là hình chữ nhật
Lời giải chi tiết:

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên tứ giác ABCD là hình bình hành.
Hình bình hành ABCD là có \(\widehat A = {90^o}\)
Do đó, tứ giác ABCD là hình chữ nhật.
Video hướng dẫn giải
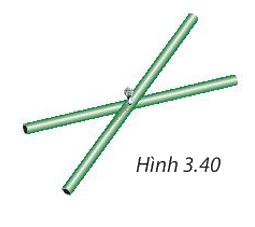
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
Phương pháp giải:
Nhận xét về hai thanh tre tạo thành hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.
Mục 2 trang 65, 66 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Các bài tập trong mục này yêu cầu học sinh vận dụng các quy tắc cộng, trừ, nhân, chia đa thức để rút gọn biểu thức, tìm giá trị của biểu thức tại một giá trị cụ thể của biến, và giải các bài toán thực tế liên quan.
Để giải tốt các bài tập trong Mục 2, học sinh cần nắm vững các kiến thức sau:
a) (3x + 2y) + (5x - y)
Giải: (3x + 2y) + (5x - y) = 3x + 2y + 5x - y = (3x + 5x) + (2y - y) = 8x + y
b) (2x - 3y) - (x + y)
Giải: (2x - 3y) - (x + y) = 2x - 3y - x - y = (2x - x) + (-3y - y) = x - 4y
a) 2x(x - 3) + 5x(x + 1)
Giải: 2x(x - 3) + 5x(x + 1) = 2x2 - 6x + 5x2 + 5x = (2x2 + 5x2) + (-6x + 5x) = 7x2 - x
b) (x + 2)(x - 2) + x2
Giải: (x + 2)(x - 2) + x2 = x2 - 4 + x2 = 2x2 - 4
P = 3x2 - 2x + 1
Giải: P = 3(-1)2 - 2(-1) + 1 = 3(1) + 2 + 1 = 3 + 2 + 1 = 6
Trong quá trình giải bài tập, học sinh cần chú ý những điều sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi làm bài tập về đa thức. Chúc các em học tập tốt!