Chào mừng bạn đến với bài học về Lý thuyết Hai tam giác đồng dạng trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Đây là một trong những kiến thức quan trọng giúp bạn giải quyết các bài toán hình học một cách hiệu quả.
Bài học này sẽ cung cấp cho bạn những khái niệm cơ bản, các trường hợp đồng dạng của tam giác, và các ứng dụng thực tế của lý thuyết này. Chúng tôi cam kết mang đến cho bạn một trải nghiệm học tập thú vị và hiệu quả.
Hai tam giác đồng dạng là gì?
1. Định nghĩa
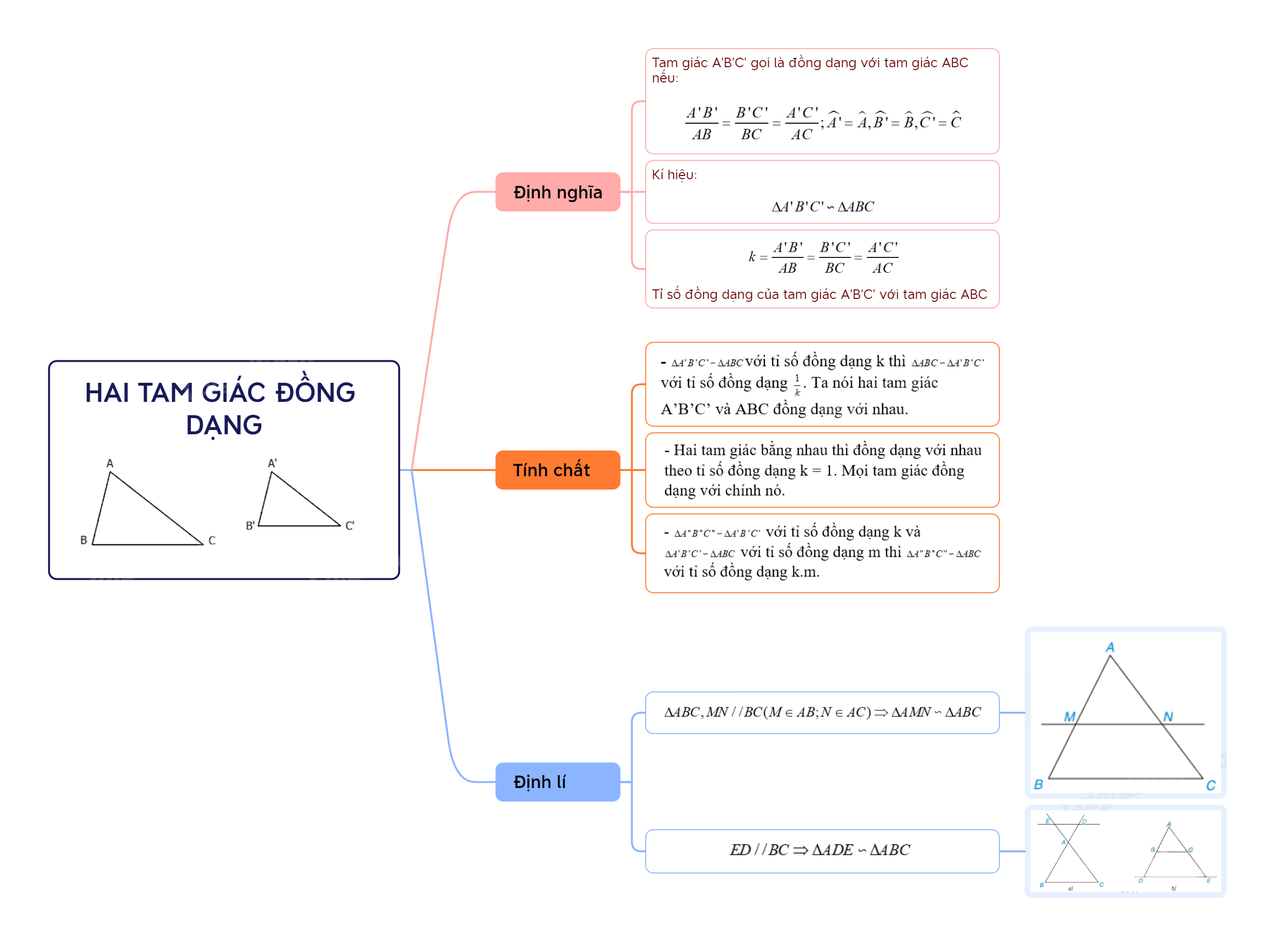
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
\(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}};\widehat {A'} = \widehat A,\widehat {B'} = \widehat B,\widehat {C'} = \widehat C\)
Kí hiệu: \(\Delta A'B'C' \backsim \Delta ABC\) (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số \(k = \frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) là tỉ số đồng dạng của \(\Delta A'B'C'\) với \(\Delta ABC\).
Nhận xét:
- \(\Delta A'B'C' \backsim \Delta ABC\)với tỉ số đồng dạng k thì \(\Delta ABC \backsim \Delta A'B'C'\) với tỉ số đồng dạng \(\frac{1}{k}\). Ta nói hai tam giác A’B’C’ và ABC đồng dạng với nhau.
- Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Mọi tam giác đồng dạng với chính nó.
- \(\Delta A''B''C'' \backsim \Delta A'B'C'\) với tỉ số đồng dạng k và \(\Delta A'B'C' \backsim \Delta ABC\) với tỉ số đồng dạng m thì \(\Delta A''B''C'' \backsim \Delta ABC\) với tỉ số đồng dạng k.m.
2. Định lí
Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
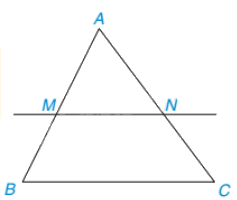
\(\Delta ABC,MN//BC(M \in AB;N \in AC) \Rightarrow \Delta AMN \backsim \Delta ABC\)
Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác.
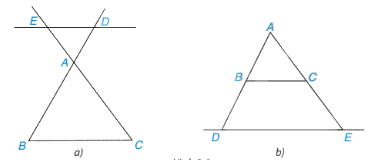
\(ED//BC \Rightarrow \Delta ADE \backsim \Delta ABC\)
Trong chương trình Toán 8, chương Hai tam giác đồng dạng đóng vai trò quan trọng trong việc phát triển tư duy hình học và khả năng giải quyết vấn đề. Bài viết này sẽ trình bày chi tiết lý thuyết về hai tam giác đồng dạng, bao gồm định nghĩa, các trường hợp đồng dạng, và các ứng dụng thực tế, dựa trên sách giáo khoa Toán 8 - Kết nối tri thức.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C' (đọc là tam giác ABC đồng dạng với tam giác A'B'C').
Điều kiện cần và đủ để hai tam giác ABC và A'B'C' đồng dạng là:
Có ba trường hợp đồng dạng của tam giác thường được sử dụng:
Nếu hai tam giác đồng dạng thì:
Lý thuyết tam giác đồng dạng có nhiều ứng dụng trong thực tế, ví dụ:
Ví dụ 1: Cho tam giác ABC có AB = 4cm, BC = 6cm, CA = 8cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có cạnh A'B' = 6cm. Tính độ dài các cạnh B'C' và C'A'.
Giải: Vì ΔABC ~ ΔA'B'C' nên ta có:
AB/A'B' = BC/B'C' = CA/C'A'
Thay số: 4/6 = 6/B'C' = 8/C'A'
Suy ra: B'C' = (6 * 6)/4 = 9cm và C'A' = (8 * 6)/4 = 12cm
Để nắm vững lý thuyết hai tam giác đồng dạng, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn để luyện tập và củng cố kiến thức.
Lý thuyết hai tam giác đồng dạng là một phần quan trọng của chương trình Toán 8. Việc hiểu rõ lý thuyết và các ứng dụng của nó sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả và tự tin hơn. Chúc bạn học tập tốt!