Bài 7.20 trang 45 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các góc trong tam giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và phương pháp giải bài tập này một cách hiệu quả.
Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay sau đây!
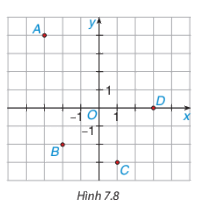
a) Xác định tọa độ của các điểm A, B, C, D trong Hình 7.8
Đề bài
a) Xác định tọa độ của các điểm A, B, C, D trong Hình 7.8
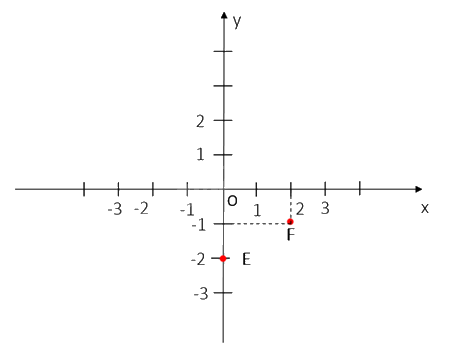
b) Xác định các điểm E (0;-2) và F (2;-1) trong Hình 7.8
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Quan sát hình 7.8 và thực hiện các yêu cầu của bài toán
Lời giải chi tiết
a) Có A(-3;4), B(-2;-2), C(1;-3), D(3;0)
b)
Bài 7.20 trang 45 SGK Toán 8 tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán các góc trong một tam giác. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản về tổng ba góc trong một tam giác (luôn bằng 180 độ) và các tính chất của tam giác cân, tam giác đều.
Đề bài thường mô tả một tình huống thực tế, ví dụ như một chiếc cầu, một mái nhà, hoặc một hình vẽ phức tạp. Học sinh cần đọc kỹ đề bài để xác định được các yếu tố quan trọng như các góc đã cho, các cạnh bằng nhau (nếu có), và yêu cầu của bài toán (tính góc, chứng minh tính chất, v.v.).
Để giải bài toán này, học sinh có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, các phép tính, và giải thích rõ ràng. Ví dụ:
Giả sử đề bài yêu cầu tính góc ABC trong tam giác ABC, biết góc BAC = 60 độ và góc ACB = 80 độ.
Ta có: Góc ABC = 180 độ - (góc BAC + góc ACB) = 180 độ - (60 độ + 80 độ) = 40 độ.
Vậy, góc ABC = 40 độ.
)Để củng cố kiến thức và kỹ năng giải bài toán, học sinh có thể luyện tập thêm các bài tập tương tự. Dưới đây là một số ví dụ:
Khi giải bài toán về góc trong tam giác, học sinh cần lưu ý những điều sau:
Kiến thức về góc trong tam giác có ứng dụng rộng rãi trong thực tế, chẳng hạn như trong kiến trúc, xây dựng, hàng hải, và các lĩnh vực khoa học khác. Ví dụ, kiến trúc sư sử dụng kiến thức này để thiết kế các công trình có độ bền vững và thẩm mỹ cao. Kỹ sư xây dựng sử dụng kiến thức này để tính toán các góc độ và kích thước của các bộ phận công trình.
Bài 7.20 trang 45 SGK Toán 8 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các góc trong tam giác. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các phương pháp giải phù hợp, học sinh có thể giải quyết bài toán này một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và kỹ năng của mình nhé!