Bài 3.44 trang 74 SGK Toán 8 tập 1 thuộc chương 3: Các góc ở vị trí đặc biệt được tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.44 trang 74 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
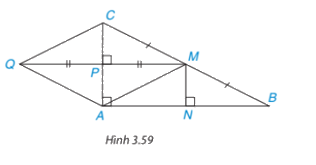
Cho tam giác ABC vuông tại A.
Đề bài
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC còn P, N lần lượt là chân đường vuông góc hạ từ M xuống CA, AB (H.3.59)
a) Chứng minh hai tam giác vuông CMP và MBN bằng nhau
b) Chứng minh tứ giác APMN là một hình chữ nhật. Từ đó suy ra N là trung điểm của AB, P là trung điểm của AC
c) Lấy điểm Q sao cho P là trung điểm của MQ, chứng minh rằng tứ giác AMCQ là một hình thoi
d) Nếu AB = AC, tức là tam giác ABC vuông cân tại A thì tứ giác AMCQ có là hình vuông không? Vì sao?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh: ΔCMP=ΔMBN (cạnh huyền – góc nhọn)
b) Chứng minh APMN có ba góc vuông nên là hình chữ nhật, dựa vào tính chất của của hình chữ nhật suy ra các cặp cạnh song song, suy ra N, P là trung điểm của AB, AC.
c) Chứng minh AMCQ có hai đường chéo vuông góc với nhau.
d) Chứng minh hình thoi AMCQ có \(\widehat {AMC} = {90^o}\) nên AMCQ là hình vuông.
Lời giải chi tiết
a) Ta có MP⊥AC, AB⊥AC suy ra MP//AB nên \(\widehat {CMP} = \widehat B\)
Xét tam giác vuông CMP và MBN ta có:
CM = MB (gt)
\(\widehat {CMP} = \widehat B\)
Suy ra ΔCMP=ΔMBN (cạnh huyền – góc nhọn)
b) Xét tứ giác APMN có \(\widehat P = \widehat A = \widehat N = {90^o}\)suy ra APMN là hình chữ nhật
Xét tam giác ABC có: M là trung điểm AB, MP//AB suy ra P là trung điểm AC
Tương tự ta có: M là trung điểm AB, MN//AC suy ra N là trung điểm AB
c) Xét tứ giác AMCQ có: P là trung điểm MQ, P là trung điểm AC, AC⊥MQ suy ra AMCQ là hình thoi
d) Nếu ABC vuông cân tại A , AM là đường trung tuyến suy ra AM cũng là đường cao suy ra\(\widehat {AMC} = {90^o}\)
Xét hình thoi AMCQ có \(\widehat {AMC} = {90^o}\)suy ra AMCQ là hình vuông
Bài 3.44 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của các góc so le trong, đồng vị, trong cùng phía.
Cho hình vẽ sau (hình vẽ minh họa bài 3.44 SGK Toán 8 tập 1 - Kết nối tri thức). Biết a // b và ∠A1 = 40°. Tính các góc ∠A2, ∠B1, ∠B2.
Vì a // b nên:
Vậy ∠A2 = 140°, ∠B1 = 40°, ∠B2 = 140°.
Bài tập này giúp học sinh hiểu rõ hơn về mối quan hệ giữa các góc khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba. Việc nắm vững các tính chất này là rất quan trọng để giải các bài tập hình học phức tạp hơn.
Ngoài bài 3.44, SGK Toán 8 tập 1 - Kết nối tri thức còn có nhiều bài tập tương tự về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Học sinh nên luyện tập thêm các bài tập này để củng cố kiến thức và kỹ năng.
Cho hình vẽ (hình vẽ minh họa bài tập tương tự). Biết a // b và ∠C = 60°. Tính ∠D.
Hướng dẫn giải: Vì a // b nên ∠C = ∠D (hai góc đồng vị). Vậy ∠D = 60°.
Bài 3.44 trang 74 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 8. Hy vọng với lời giải chi tiết và hướng dẫn phân tích trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự tin giải các bài tập tương tự.
| Loại góc | Tính chất |
|---|---|
| So le trong | Bằng nhau |
| Đồng vị | Bằng nhau |
| Trong cùng phía | Bù nhau (tổng bằng 180°) |
Chúc các em học tốt môn Toán!