Chào mừng bạn đến với bài học lý thuyết Đa thức trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đa thức, giúp bạn tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa đa thức, các loại đa thức, cách thu gọn đa thức, bậc của đa thức và các phép toán trên đa thức. Mục tiêu là giúp bạn nắm vững kiến thức nền tảng để học tốt môn Toán.
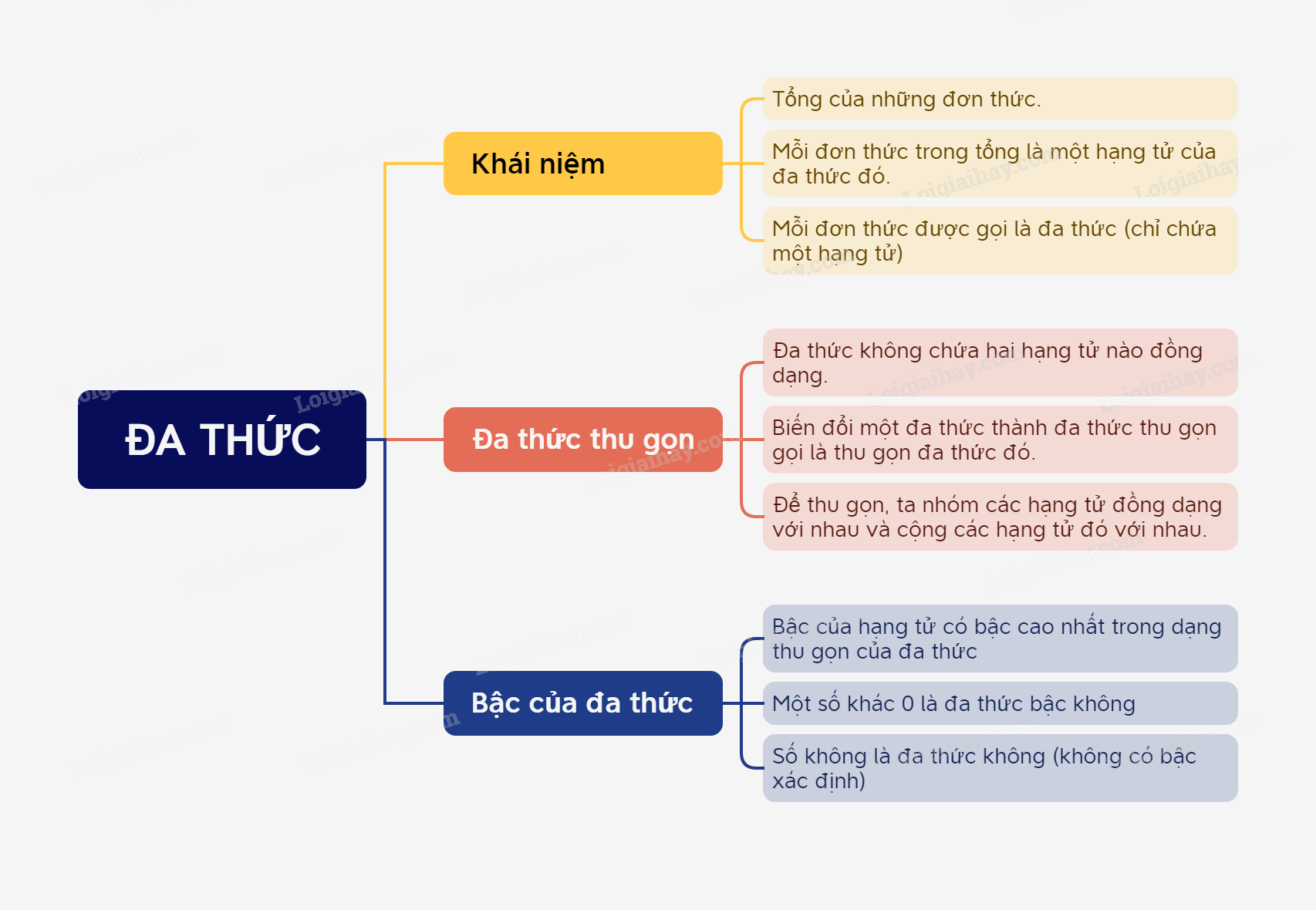
Đa thức là một tổng của những đơn thức.
Đa thức là một tổng của những đơn thức.
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ: \({x^2} - 4x + 3;{x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1;\left( {x{\rm{ }} + {\rm{ }}3y} \right){\rm{ }} + \left( {2x{\rm{ }}-{\rm{ }}y} \right)\) là đa thức.
\(\frac{{x + y}}{{x - y}},\frac{{{x^2} + 2}}{{{x^2} - {y^2}}}\) không phải là đa thức.
\({x^2} - 4x + 3\) có 3 hạng tử \({x^2}; - 4x;3\).
\({x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1\) có 4 hạng tử \({x^2}{\rm{; }}3xy{z^2};\; - {\rm{ }}yz{\rm{ ; }}1\).
Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Ví dụ:
\(\begin{array}{l}A = {x^3} - 2{x^2}y - {x^2}y + 3x{y^2} - {y^3}\\\,\,\,\,\, = {x^3} - 3{x^2}y - 3x{y^2} - {y^3}\end{array}\)
Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Một số khác 0 tùy ý được coi là một đa thức bậc 0.
Số 0 cũng là một đa thức, gọi là đa thức không. Nó không có bậc xác định.
Đa thức là một biểu thức đại số được xây dựng từ các số, các biến và các phép toán cộng, trừ, nhân, chia (với số khác 0) và lũy thừa với số mũ nguyên không âm. Hiểu rõ về đa thức là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Một đa thức là một biểu thức có dạng:
P(x) = anxn + an-1xn-1 + ... + a1x + a0
Trong đó:
Ví dụ: 3x2 + 2x - 5 là một đa thức.
Thu gọn đa thức là quá trình thực hiện các phép toán cộng, trừ các đơn thức đồng dạng để đưa đa thức về dạng đơn giản nhất.
Ví dụ: Thu gọn đa thức 2x2 + 3x - x2 + 5x - 2:
2x2 + 3x - x2 + 5x - 2 = (2x2 - x2) + (3x + 5x) - 2 = x2 + 8x - 2
Bậc của đa thức là số mũ lớn nhất của biến trong đa thức đã thu gọn.
Ví dụ:
Để hiểu rõ hơn về lý thuyết đa thức, bạn hãy thực hành giải các bài tập sau:
Hy vọng bài học này đã giúp bạn nắm vững kiến thức về lý thuyết đa thức. Chúc bạn học tốt!