Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 2 - Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 11 trang 136, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC
Đề bài
Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I. Chứng minh rằng
a) ΔBIC \(\backsim\) ΔEIF
b) \(F{B^2} = FI.FC\)
c) Cho biết AB = 6cm, BC = 3 cm. Tính EF
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh hai tam giác BIC và tam giác EIF có \(\widehat {IBC} = \widehat {IEF}{;^{}}\widehat {ICB} = \widehat {{\rm{IFE}}}\)(hai góc so le trong)
=> ΔBIC \(\backsim\) ΔEIF (g.g)
b) Sử dụng các tỉ số đồng dạng của hai tam giác để chứng minh \(F{B^2} = FI.FC\)
c) Tìm EF dựa vào định lý Thales.
Lời giải chi tiết
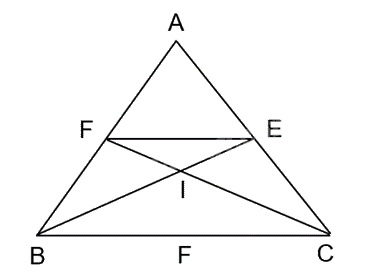
a) Vì tam giác ABC là tam giác cân
=> Hai đường phân giác đồng thời là đường trung tuyến
=> EF là đường trung bình của tam giác ABC
=> EF // BC
=> \(\widehat {IBC} = \widehat {IEF}{;^{}}\widehat {ICB} = \widehat {{\rm{IFE}}}\)(hai góc so le trong)
=> ΔBIC \(\backsim\) ΔEIF (g.g)
b) Vì tam giác ABC cân tại A
=> \(\widehat {ABE} = \widehat {EBC} = \widehat {ACF} = \widehat {FCB}\)
Xét tam giác FBI và tam giác FCB có góc F chung, $\widehat{FBI}=\widehat{FCB}$
=> ΔFBI \(\backsim\) ΔFCB (g.g)
=> \(\frac{{FB}}{{FC}} = \frac{{FI}}{{FB}}\)
=> \(F{B^2} = FI.FC\)
c) Ta có EF // BC (chứng minh trên). Do đó:
\( \frac{BC}{EF} = \frac{AB}{AF} \Rightarrow \frac{ (AF + FB)}{AF} = 1 + \frac{BC}{AB}=1+ \frac{3}{6} = \frac{3}{2} \)
Từ đó suy ra \( EF = 3 : \frac{3}{2} = 2 \) (cm)
Bài 11 trang 136 SGK Toán 8 tập 2 - Kết nối tri thức thuộc chương trình học về hình hộp chữ nhật và hình lăng trụ đứng. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm cơ bản và công thức liên quan.
Bài 11 trang 136 thường yêu cầu tính diện tích xung quanh hoặc thể tích của hình hộp chữ nhật hoặc hình lăng trụ đứng. Để giải bài toán, bạn cần:
Giả sử bài toán yêu cầu tính thể tích của một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm.
Giải:
Thể tích của hình hộp chữ nhật là: V = a.b.h = 5cm.3cm.4cm = 60cm3
Ngoài bài tập tính thể tích, bài 11 trang 136 còn có thể xuất hiện các dạng bài tập khác như:
Đối với các dạng bài tập này, bạn cần áp dụng các công thức tương ứng và thực hiện các phép tính một cách cẩn thận.
Kiến thức về hình hộp chữ nhật và hình lăng trụ đứng có ứng dụng rất lớn trong thực tế, ví dụ như tính thể tích của các vật dụng hình hộp chữ nhật (hộp quà, tủ lạnh,...) hoặc tính diện tích bề mặt của các công trình xây dựng.
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
Bài 11 trang 136 SGK Toán 8 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp bạn hiểu rõ hơn về hình hộp chữ nhật và hình lăng trụ đứng. Bằng cách nắm vững lý thuyết, phân tích bài toán và áp dụng công thức phù hợp, bạn có thể giải bài tập một cách dễ dàng và hiệu quả.
Chúc bạn học tốt!