Giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức

Bài 3.27 trang 66 SGK Toán 8 tập 1 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.27, giúp các em học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải toán.

Cho tam giác ABC, đường cao AH.

Đề bài

Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức 1

Chứng minh tứ giác AHCN là hình bình hành có \(\widehat {AHC} = {90^o}\) nên AHCN là hình chữ nhật

Lời giải chi tiết

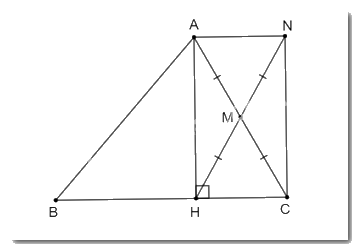
Giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức 2

Theo đề bài, M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN.

Nên tứ giác ANCH có hai đường chéo AC và HN cắt nhau tại trung điểm M của mỗi đường.

Suy ra tứ giác ANCH là hình bình hành.

Hình bình hành ANCH có \(\widehat {AHC} = {90^o}\) nên tứ giác ANCH là hình chữ nhật.

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức đặc sắc thuộc chuyên mục toán lớp 8 trên tài liệu toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Giải bài 3.27 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết và phương pháp giải

Bài 3.27 trang 66 SGK Toán 8 tập 1 yêu cầu chúng ta chứng minh một tính chất quan trọng liên quan đến các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Để giải bài này, chúng ta cần nắm vững các kiến thức cơ bản về:

Các góc so le trong: Hai góc so le trong bằng nhau.
Các góc đồng vị: Hai góc đồng vị bằng nhau.
Các góc trong cùng phía: Hai góc trong cùng phía bù nhau.

Đề bài: Cho hình vẽ, biết a // b. Chứng minh rằng góc A₁ = góc B₁.

Lời giải:

Phân tích bài toán: Để chứng minh góc A₁ = góc B₁, chúng ta cần tìm mối liên hệ giữa hai góc này với các góc khác trong hình. Ta nhận thấy góc A₁ và góc B₁ là hai góc ở vị trí so le trong đối với đường thẳng cắt a và b.
Chứng minh:

Vì a // b nên góc A₁ = góc A₂ (hai góc so le trong).
Vì a // b nên góc A₂ = góc B₁ (hai góc đồng vị).
Suy ra góc A₁ = góc B₁ (tính chất bắc cầu).

Kết luận: Vậy, góc A₁ = góc B₁.

Phương pháp giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song

Để giải các bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em học sinh cần:

Nắm vững các định nghĩa và tính chất: Các góc so le trong, đồng vị, trong cùng phía.
Xác định đúng vị trí các góc: Quan sát kỹ hình vẽ để xác định đúng vị trí của các góc.
Vận dụng linh hoạt các tính chất: Sử dụng các tính chất của các góc để chứng minh các mối quan hệ giữa chúng.
Phân tích bài toán: Xác định rõ mục tiêu của bài toán và tìm cách tiếp cận phù hợp.

Ví dụ minh họa:

Cho hình vẽ, biết a // b và góc A₁ = 60^o. Tính góc B₁.

Lời giải:

Vì a // b nên góc A₁ = góc B₁ (hai góc so le trong).

Vậy, góc B₁ = 60^o.

Luyện tập thêm

Để củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song, các em học sinh có thể luyện tập thêm các bài tập sau:

Bài 3.28 trang 66 SGK Toán 8 tập 1.
Bài 3.29 trang 66 SGK Toán 8 tập 1.
Các bài tập tương tự trong sách bài tập Toán 8 tập 1.

Tổng kết:

Bài 3.27 trang 66 SGK Toán 8 tập 1 là một bài tập quan trọng giúp các em học sinh hiểu rõ và vận dụng các kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng song song. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!