Bài 7.29 trang 50 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng định lý về đường trung bình của tam giác vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.29 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất
Đề bài
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y=ax+b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.
a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày
b) Vẽ đồ thị hàm số thu được ở câu a
c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu
d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày: y=1,8x+36
b) Xác định hai điểm thuộc đồ thị hàm số y = 1,8 x + 36 để vẽ đồ thị hàm số.
c) thay x = 15 vào công thức hàm số y = 1,8 x + 36 để tính chi phí sản xuất 15 chiếc xe đạp.
d) Thay y = 72 vào công thức hàm số y = 1,8x + 36 tìm ra x để tính có thể sản xuất bao nhiêu chiếc xe đạp trong ngày.
Lời giải chi tiết
a) Công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày: y=1,8x+36
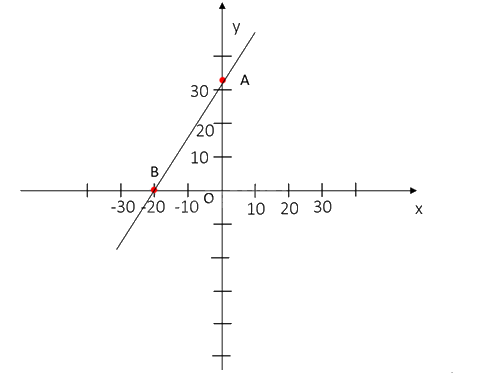
b) Cho x=0 thì y=36 ta có A(0;36)
y=0 thì x=-20, ta có B(-20;0)
Đồ thị của hàm số là đường thẳng AB
c) Chi phí để sản xuất 15 chiếc xe đạp trong 1 ngày là: y=1,8.15+36=63 (triệu)
d) 72=1,8x+36 => x=20 (chiếc xe)
Bài 7.29 yêu cầu chúng ta sử dụng kiến thức về đường trung bình của tam giác để chứng minh một số tính chất hình học. Để giải bài này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm và định lý liên quan.
Trước khi đi vào giải chi tiết, hãy đọc kỹ đề bài và xác định những yếu tố đã cho và những điều cần chứng minh. Thông thường, bài toán sẽ cung cấp một hình vẽ hoặc mô tả về một tam giác, và yêu cầu chúng ta chứng minh một mối quan hệ nào đó giữa các đoạn thẳng trong hình.
Đề bài: (Giả sử đề bài cụ thể được đưa ra ở đây. Ví dụ: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Chứng minh MN song song với BC và MN = 1/2 BC.)
Lời giải:
Để hiểu rõ hơn về cách áp dụng định lý đường trung bình của tam giác, chúng ta hãy xem xét một ví dụ minh họa sau:
Ví dụ: Cho tam giác DEF, P là trung điểm của DE, Q là trung điểm của DF. Biết EF = 8cm. Tính độ dài PQ.
Lời giải: Vì P, Q lần lượt là trung điểm của DE, DF, nên PQ là đường trung bình của tam giác DEF. Do đó, PQ = 1/2 EF = 1/2 * 8cm = 4cm.
Ngoài bài 7.29, các em có thể tham khảo thêm một số bài tập tương tự sau:
Định lý về đường trung bình của tam giác không chỉ được áp dụng trong việc giải các bài toán hình học cơ bản mà còn có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc thiết kế các công trình xây dựng, đo đạc khoảng cách, và nhiều lĩnh vực khác.
Khi giải các bài tập liên quan đến đường trung bình của tam giác, các em cần chú ý:
Bài 7.29 trang 50 SGK Toán 8 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp các em củng cố kiến thức về đường trung bình của tam giác. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải các bài tập tương tự.