Chào mừng bạn đến với bài học về Lý thuyết Phép nhân đa thức trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về phép nhân đa thức, giúp bạn tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các quy tắc, tính chất và phương pháp áp dụng phép nhân đa thức một cách chi tiết và dễ hiểu nhất.
1. Nhân đơn thức với đa thức
1. Nhân đơn thức với đa thức
+ Nhân hai đơn thức như thế nào?
Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.
Ví dụ: \(( - 3{x^2}y)(4xy) = \left[ {\left( { - 3.4} \right)} \right].({x^2}.x).\left( {y.y} \right) = - 12.{x^3}.{y^2}\)
+ Nhân đơn thức với đa thức như thế nào?
Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
Ví dụ:
\(\begin{array}{l}3{x^2}y\left( {2{x^2}y - xy + 3{y^2}} \right)\\ = (3{x^2}y).(2{x^2}y) - (3{x^2}y).(xy) + (3{x^2}y).(3{y^2})\\ = 3.2.({x^2}.{x^2})\left( {y.y} \right) - 3.({x^2}.x).\left( {y.y} \right) + 3.3.{x^2}.\left( {y.{y^2}} \right)\\ = 6{x^4}{y^2} - 3{x^3}.{y^2} + 9{x^2}{y^3}\end{array}\)
2. Nhân đa thức với đa thức
+ Nhân hai đa thức như thế nào?
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Phép nhân đa thức cũng có các tính chất tương tự phép nhân các số.
+ Giao hoán: A.B = B.A
+ Kết hợp: (A.B).C = A.(B.C)
+ Phân phối của phép nhân đối với phép cộng: (A + B).C = AB + AC
Ví dụ:
\(\begin{array}{l}(xy + 1)(xy - 3)\\ = (xy).\left( {xy} \right) + xy - 3xy - 3\\ = {x^2}{y^2} - 2xy - 3\end{array}\)
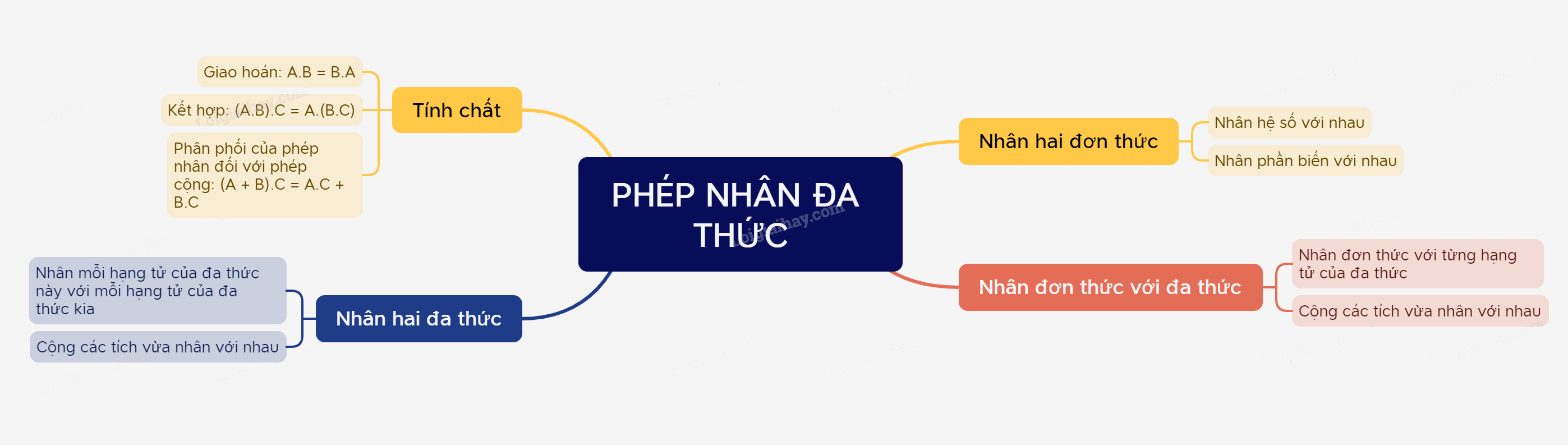
Phép nhân đa thức là một trong những phép toán cơ bản và quan trọng trong đại số lớp 8. Việc nắm vững lý thuyết và kỹ năng thực hành phép nhân đa thức là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Phép nhân đa thức là phép toán thực hiện nhân hai hoặc nhiều đa thức với nhau. Kết quả của phép nhân đa thức là một đa thức mới.
Để nhân hai đa thức, ta thực hiện các bước sau:
Công thức tổng quát:
(a + b)(c + d) = ac + ad + bc + bd
Ví dụ 1: Tính (2x + 3)(x - 1)
(2x + 3)(x - 1) = 2x(x - 1) + 3(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Ví dụ 2: Tính (x2 + 2x - 1)(x + 2)
(x2 + 2x - 1)(x + 2) = x2(x + 2) + 2x(x + 2) - 1(x + 2) = x3 + 2x2 + 2x2 + 4x - x - 2 = x3 + 4x2 + 3x - 2
Hãy thực hiện các phép nhân đa thức sau:
Trong quá trình học tập và làm việc, bạn sẽ gặp nhiều bài toán phức tạp hơn liên quan đến phép nhân đa thức. Để giải quyết những bài toán này, bạn cần nắm vững các kiến thức cơ bản và rèn luyện kỹ năng thực hành thường xuyên.
Ngoài ra, bạn có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả và tiết kiệm thời gian.
Hy vọng bài học về Lý thuyết Phép nhân đa thức SGK Toán 8 - Kết nối tri thức này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập môn Toán. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất!
| Đa thức 1 | Đa thức 2 | Kết quả |
|---|---|---|
| x + 2 | x - 3 | x2 - x - 6 |
| 2x - 1 | x + 4 | 2x2 + 7x - 4 |