Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 50, 51 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng của tứ giác ABCD.
Video hướng dẫn giải
Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?
Phương pháp giải:
Áp dụng định lí tổng các góc trong một tứ giác
Lời giải chi tiết:
• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90o).
Khi đó, tổng 4 góc nhỏ hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong tứ giác bằng 360o).
• Nếu tứ giác có 3 góc nhọn (nhỏ hơn 90o); 1 góc tù (góc lớn hơn 90o).
Khi đó, tổng 3 góc nhọn nhỏ hơn: 3 . 90o = 270o;
Số đo góc còn lại lớn hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc nhọn.
• Nếu 4 góc tứ giác đều tù (mỗi góc lớn hơn 90o).
Khi đó, tổng 4 góc lớn hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong một tứ giác bằng 360o).
• Nếu tứ giác có 3 góc tù và 1 góc nhọn.
Tổng 3 góc tù lớn hơn: 3.90o = 270o;
Số đo góc còn lại của tứ giác nhỏ hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc tù.
Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.
Video hướng dẫn giải
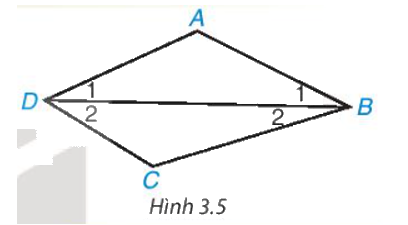
Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng các góc của tứ giác ABCD.
Phương pháp giải:
Vận dụng định lí tổng ba góc trong một tam giác
Lời giải chi tiết:
Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
\(\begin{array}{l}\widehat A + \widehat {{B_1}} + \widehat {{D_1}} = {180^o}\\\widehat C + \widehat {{B_2}} + \widehat {{D_2}} = {180^o}\end{array}\)
Khi đó, tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = \widehat A + \widehat {{B_1}} + \widehat {{D_1}} + \widehat C + \widehat {{B_2}} + \widehat {{D_2}} = 180^\circ + 180^\circ = 360^\circ \)
Vậy \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Video hướng dẫn giải
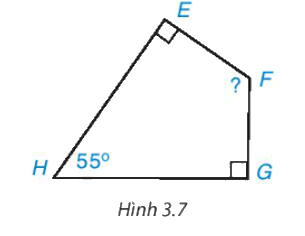
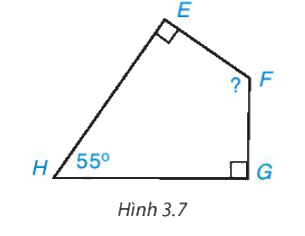
Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.
Phương pháp giải:
Vận dụng định lí tổng các góc trong một tứ giác.
Lời giải chi tiết:
Xét tứ giác EFGH có:
\(\) \(\widehat E + \widehat F + \widehat G + \widehat H = {360^o}\)(định lí tổng các góc trong một tứ giác).
Hay \({90^o} + \widehat F + {90^o} + {55^o} = {360^o}\)
Suy ra \(\widehat F\)+235°=360°
Do đó \(\widehat F\)=360°−235°=125°
Vậy \(\widehat F\)=125o
Video hướng dẫn giải
Câu hỏi mở đầu
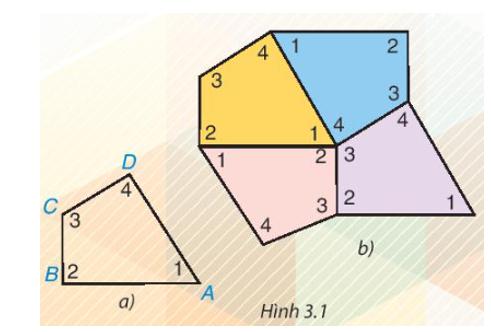
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
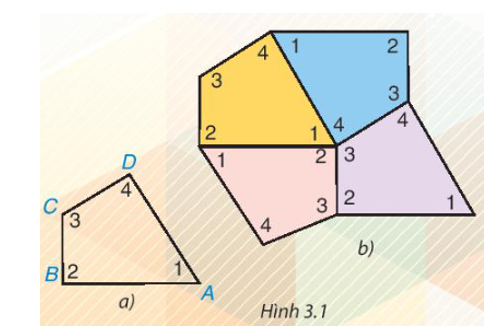
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo.
Phương pháp giải:
Quan sát hình 3.4 và nhận xét
Lời giải chi tiết:
Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Video hướng dẫn giải
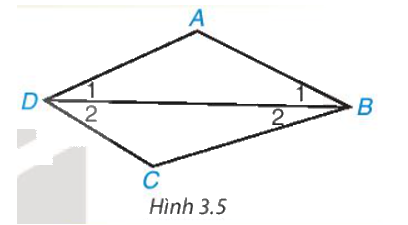
Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng các góc của tứ giác ABCD.
Phương pháp giải:
Vận dụng định lí tổng ba góc trong một tam giác
Lời giải chi tiết:
Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
\(\begin{array}{l}\widehat A + \widehat {{B_1}} + \widehat {{D_1}} = {180^o}\\\widehat C + \widehat {{B_2}} + \widehat {{D_2}} = {180^o}\end{array}\)
Khi đó, tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = \widehat A + \widehat {{B_1}} + \widehat {{D_1}} + \widehat C + \widehat {{B_2}} + \widehat {{D_2}} = 180^\circ + 180^\circ = 360^\circ \)
Vậy \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Video hướng dẫn giải
Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.
Phương pháp giải:
Vận dụng định lí tổng các góc trong một tứ giác.
Lời giải chi tiết:
Xét tứ giác EFGH có:
\(\) \(\widehat E + \widehat F + \widehat G + \widehat H = {360^o}\)(định lí tổng các góc trong một tứ giác).
Hay \({90^o} + \widehat F + {90^o} + {55^o} = {360^o}\)
Suy ra \(\widehat F\)+235°=360°
Do đó \(\widehat F\)=360°−235°=125°
Vậy \(\widehat F\)=125o
Video hướng dẫn giải
Câu hỏi mở đầu
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo.
Phương pháp giải:
Quan sát hình 3.4 và nhận xét
Lời giải chi tiết:
Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
Video hướng dẫn giải
Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?
Phương pháp giải:
Áp dụng định lí tổng các góc trong một tứ giác
Lời giải chi tiết:
• Nếu 4 góc trong tứ giác đều nhọn (mỗi góc nhỏ hơn 90o).
Khi đó, tổng 4 góc nhỏ hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong tứ giác bằng 360o).
• Nếu tứ giác có 3 góc nhọn (nhỏ hơn 90o); 1 góc tù (góc lớn hơn 90o).
Khi đó, tổng 3 góc nhọn nhỏ hơn: 3 . 90o = 270o;
Số đo góc còn lại lớn hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc nhọn.
• Nếu 4 góc tứ giác đều tù (mỗi góc lớn hơn 90o).
Khi đó, tổng 4 góc lớn hơn: 4 . 90o = 360o (vô lí vì tổng 4 góc trong một tứ giác bằng 360o).
• Nếu tứ giác có 3 góc tù và 1 góc nhọn.
Tổng 3 góc tù lớn hơn: 3.90o = 270o;
Số đo góc còn lại của tứ giác nhỏ hơn: 360o – 270o = 90o (thỏa mãn).
Do đó, một tứ giác có thể có nhiều nhất 3 góc tù.
Vậy một tứ giác có thể có nhiều nhất 3 góc nhọn; một tứ giác có thể có nhiều nhất 3 góc tù.
Mục 2 của chương trình Toán 8 tập 1 Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về đa thức. Cụ thể, học sinh sẽ được làm quen với các khái niệm như đơn thức, đa thức, bậc của đa thức, các phép toán trên đa thức (cộng, trừ, nhân, chia) và các ứng dụng của chúng trong giải toán.
Bài tập trong mục 2 trang 50, 51 SGK Toán 8 tập 1 Kết nối tri thức bao gồm nhiều dạng bài khác nhau, từ các bài tập đơn giản về nhận biết đơn thức, đa thức đến các bài tập phức tạp hơn về thực hiện các phép toán trên đa thức và ứng dụng chúng để giải các bài toán thực tế.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép cộng, trừ các đơn thức đồng dạng. Để thu gọn đa thức, học sinh cần xác định các đơn thức đồng dạng và cộng, trừ các hệ số của chúng.
Ví dụ: Thu gọn đa thức 3x2 + 2x - 5x2 + x + 1.
Giải:
Bài tập này yêu cầu học sinh tìm bậc của các đa thức đã cho. Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó.
Ví dụ: Tìm bậc của đa thức 2x3 - 5x2 + x - 1.
Giải:
Bậc của đơn thức 2x3 là 3; bậc của đơn thức -5x2 là 2; bậc của đơn thức x là 1; bậc của đơn thức -1 là 0.
Vậy bậc của đa thức 2x3 - 5x2 + x - 1 là 3.
Bài tập này yêu cầu học sinh thực hiện các phép cộng, trừ đa thức. Để thực hiện các phép toán này, học sinh cần cộng, trừ các đơn thức đồng dạng trong hai đa thức.
Ví dụ: Thực hiện phép cộng hai đa thức A = 2x2 + 3x - 1 và B = -x2 + x + 2.
Giải:
A + B = (2x2 + 3x - 1) + (-x2 + x + 2) = (2x2 - x2) + (3x + x) + (-1 + 2) = x2 + 4x + 1.
Kiến thức về đa thức có nhiều ứng dụng trong giải toán và trong thực tế. Ví dụ, đa thức có thể được sử dụng để mô tả các đại lượng thay đổi, để giải các phương trình bậc hai, bậc ba, và để tính diện tích, thể tích của các hình học.
Hy vọng bài giải chi tiết mục 2 trang 50, 51 SGK Toán 8 tập 1 - Kết nối tri thức này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải toán liên quan đến đa thức. Chúc các em học tập tốt!