Định lí Pythagore là một trong những định lý quan trọng nhất trong hình học, được học trong chương trình Toán 8 - Kết nối tri thức. Nó mô tả mối quan hệ giữa các cạnh của một tam giác vuông và có ứng dụng rộng rãi trong thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ và dễ hiểu về định lý này, giúp bạn nắm vững kiến thức nền tảng và tự tin giải các bài tập.
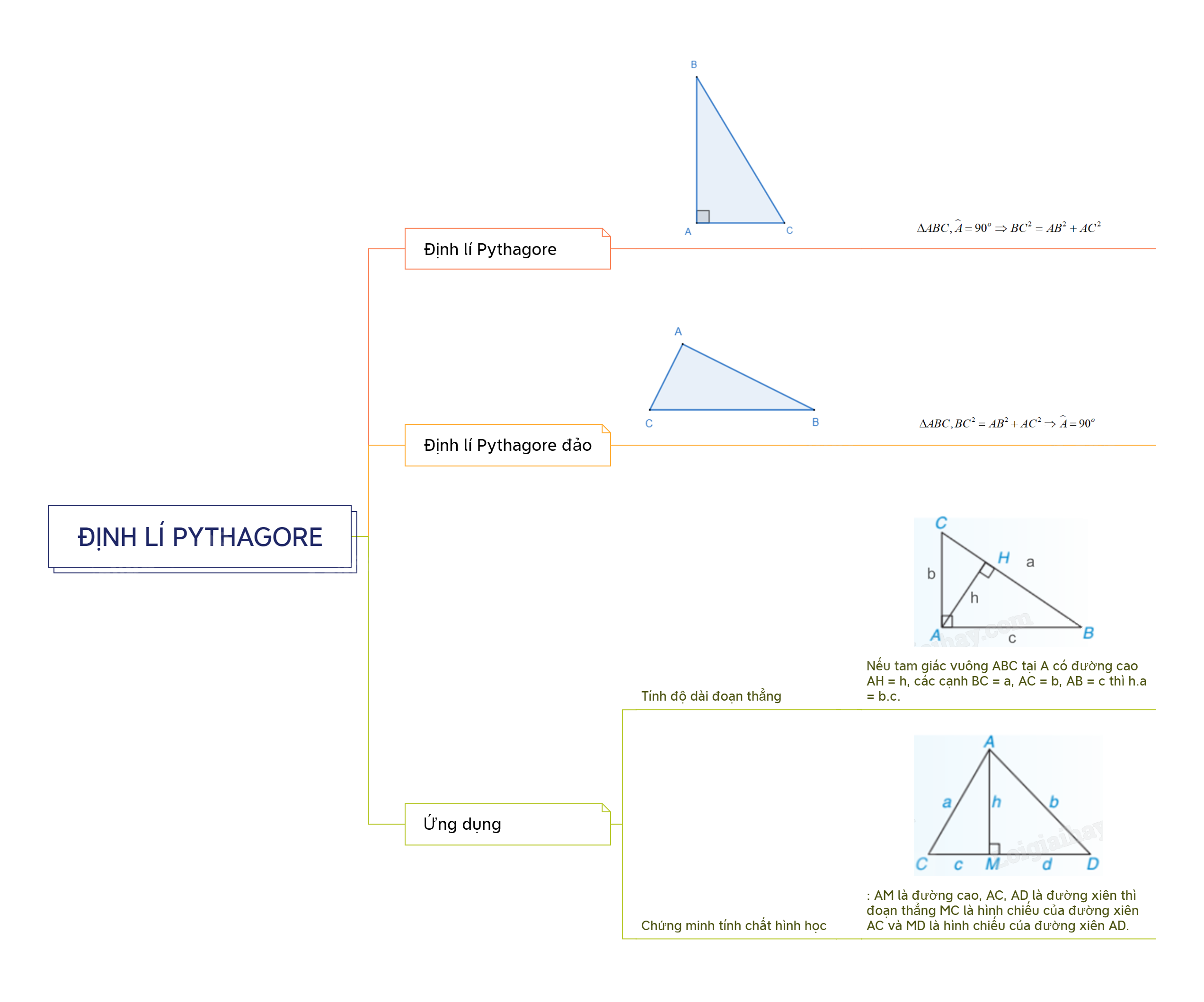
Định lí Pythagore là gì?
1. Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
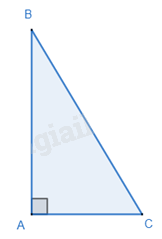
\(\Delta ABC,\widehat A = {90^o} \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \(B{C^2} = A{B^2} + A{C^2}\).
2. Định lí Pythagore đảo
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
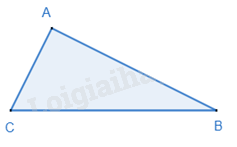
\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat A = {90^o}\)
3. Ứng dụng của định lí Pythagore
a. Tính độ dài đoạn thẳng
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.
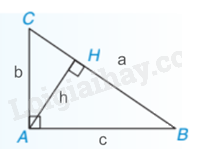
Ví dụ: Tam giác ABC vuông tại A có AB = 5cm, AC = 12cm thì BC = \(\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\)
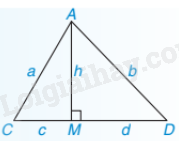
b. Chứng minh tính chất hình học
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.
Định lí Pythagore là nền tảng của hình học tam giác vuông, một khái niệm quan trọng trong chương trình Toán 8 - Kết nối tri thức. Bài viết này sẽ cung cấp một cái nhìn toàn diện về định lý này, bao gồm phát biểu, chứng minh, và các ứng dụng thực tế.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Công thức toán học biểu diễn định lý này là: a2 + b2 = c2, trong đó 'c' là cạnh huyền và 'a', 'b' là hai cạnh góc vuông.
Có nhiều cách chứng minh Định lí Pythagore. Một trong những cách phổ biến nhất là sử dụng diện tích. Chúng ta có thể xây dựng một hình vuông lớn với cạnh bằng (a + b). Bên trong hình vuông này, chúng ta có thể tạo ra bốn tam giác vuông bằng nhau với các cạnh a, b, và c, cùng với một hình vuông nhỏ ở giữa có cạnh c. Diện tích của hình vuông lớn bằng tổng diện tích của bốn tam giác vuông và diện tích của hình vuông nhỏ. Từ đó, ta có thể suy ra công thức a2 + b2 = c2.
Định lí Pythagore có rất nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học:
SGK Toán 8 - Kết nối tri thức cung cấp nhiều bài tập vận dụng Định lí Pythagore với các mức độ khó khác nhau. Dưới đây là một số ví dụ:
Định lí Pythagore có thể được mở rộng cho các không gian nhiều chiều. Ví dụ, trong không gian ba chiều, công thức tổng quát hóa của Định lí Pythagore là: d2 = x2 + y2 + z2, trong đó 'd' là khoảng cách giữa hai điểm trong không gian, và 'x', 'y', 'z' là các tọa độ của hai điểm đó.
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn đầy đủ và chi tiết về Lý thuyết Định lí Pythagore và ứng dụng SGK Toán 8 - Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài tập.