Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 51, 52 sách giáo khoa Toán 8 tập 2 chương trình Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, chính xác, cùng với phương pháp giải dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và phù hợp với chương trình học hiện hành. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng sau:
Video hướng dẫn giải
Từ kết quả của hoạt động 1, em có nhận xét gì về quan hệ giữa hệ số a của đường thẳng y=ax+b (a≠0) với góc tạo bởi đường thẳng này và trục Ox
Phương pháp giải:
Quan sát hình vẽ từ hoạt động 1
Lời giải chi tiết:
Khi hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn Khi hệ số góc a âm thì góc tạo bởi đường thẳng này và trục Ox là góc tù.
Video hướng dẫn giải
Xác định hệ số góc của mỗi đường thẳng sau:
\(y = 3{\rm{x}} - 1\); \(y = 2 - x\); \(y = \frac{1}{2}\left( {x - 1} \right)\)
Phương pháp giải:
Hệ số góc của đường thẳng \(y = {\rm{ax + b }}\left( {a \ne 0} \right)\) là a
Lời giải chi tiết:
Hệ số góc của đường thẳng \(y = 3{\rm{x}} - 1\) là a = 3.
Hệ số góc của đường thẳng \(y = 2 - x\) là a = -1
Hệ số góc của đường thẳng \(y = \frac{1}{2}\left( {x - 1} \right) = \frac{1}{2}x - \frac{1}{2}\) là \(a = \frac{1}{2}\)
Video hướng dẫn giải
Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là 3 và cắt trục tung tại điểm có tung độ bằng -1
Phương pháp giải:
Xác định a , b của hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Hàm số có hệ số góc bằng 3 nên hàm số bậc nhất cần tìm là: y = 3x + b
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng -1 nên ta thay điểm (0; -1) vào công thức hàm số y = 3x + b ta được: b = -1
Vậy hàm số bậc nhất đó là: y=3x−1
Video hướng dẫn giải
Đường thẳng \(y = \frac{{2{\rm{x}} + 1}}{2}\) có hệ số góc bằng bao nhiêu?
Tròn: Đường thẳng này có hệ số góc a = 2
Vuông: Không đúng, đường thẳng này có hệ số góc a = 1
Theo em, bạn nào trả lời đúng, bạn nào trả lời sai? Vì sao?
Phương pháp giải:
Biến đổi hàm số \(y = \frac{{2{\rm{x}} + 1}}{2} = \frac{{2{\rm{x}}}}{2} + \frac{1}{2} = x + \frac{1}{2}\) từ đó xác định được hệ số góc và tìm ra được bạn nào đúng, bạn nào sai.
Lời giải chi tiết:
Ta có: \(y = \frac{{2{\rm{x}} + 1}}{2} = \frac{{2{\rm{x}}}}{2} + \frac{1}{2} = x + \frac{1}{2}\)
Hệ số góc của đường thẳng \(y = \frac{{2{\rm{x}} + 1}}{2}\) là \(a = 1\).
Như vậy bạn tròn sai và bạn vuông đúng.
Video hướng dẫn giải
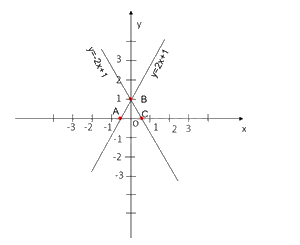
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng sau:
(d): y=2x+1 và (d'): y=−2x+1
a) So sánh góc tạo bởi đường thẳng (d) và trục Ox với 90°
b) So sánh góc tạo bởi đường thẳng (d') và trục Ox với 90°
Phương pháp giải:
Xác định hai điểm thuộc đường thẳng d và d’ để vẽ hai đường thẳng d và d’ trong mặt phẳng tọa độ.
Từ hình vẽ đồ thị hàm số d và d’ so sánh với góc 90o
Lời giải chi tiết:
Xét (d): y=2x+1:
Cho y=0 thì \(x = \frac{{ - 1}}{2}\), ta được giao điểm của đồ thị với trục Ox là A(\(\frac{{ - 1}}{2};0\))
x=0 thì y=1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Xét (d'): y=−2x+1:
Cho y=0 thì \(x = \frac{1}{2}\), ta được giao điểm của đồ thị với trục Ox là \(C\left( {\frac{1}{2};0} \right)\)
x=0 thì y=1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Video hướng dẫn giải
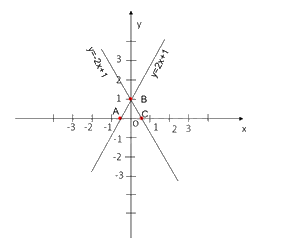
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng sau:
(d): y=2x+1 và (d'): y=−2x+1
a) So sánh góc tạo bởi đường thẳng (d) và trục Ox với 90°
b) So sánh góc tạo bởi đường thẳng (d') và trục Ox với 90°
Phương pháp giải:
Xác định hai điểm thuộc đường thẳng d và d’ để vẽ hai đường thẳng d và d’ trong mặt phẳng tọa độ.
Từ hình vẽ đồ thị hàm số d và d’ so sánh với góc 90o
Lời giải chi tiết:
Xét (d): y=2x+1:
Cho y=0 thì \(x = \frac{{ - 1}}{2}\), ta được giao điểm của đồ thị với trục Ox là A(\(\frac{{ - 1}}{2};0\))
x=0 thì y=1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Xét (d'): y=−2x+1:
Cho y=0 thì \(x = \frac{1}{2}\), ta được giao điểm của đồ thị với trục Ox là \(C\left( {\frac{1}{2};0} \right)\)
x=0 thì y=1, ta được giao điểm của đồ thị với trục Oy là B(0;1)
Video hướng dẫn giải
Từ kết quả của hoạt động 1, em có nhận xét gì về quan hệ giữa hệ số a của đường thẳng y=ax+b (a≠0) với góc tạo bởi đường thẳng này và trục Ox
Phương pháp giải:
Quan sát hình vẽ từ hoạt động 1
Lời giải chi tiết:
Khi hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn Khi hệ số góc a âm thì góc tạo bởi đường thẳng này và trục Ox là góc tù.
Video hướng dẫn giải
Xác định hệ số góc của mỗi đường thẳng sau:
\(y = 3{\rm{x}} - 1\); \(y = 2 - x\); \(y = \frac{1}{2}\left( {x - 1} \right)\)
Phương pháp giải:
Hệ số góc của đường thẳng \(y = {\rm{ax + b }}\left( {a \ne 0} \right)\) là a
Lời giải chi tiết:
Hệ số góc của đường thẳng \(y = 3{\rm{x}} - 1\) là a = 3.
Hệ số góc của đường thẳng \(y = 2 - x\) là a = -1
Hệ số góc của đường thẳng \(y = \frac{1}{2}\left( {x - 1} \right) = \frac{1}{2}x - \frac{1}{2}\) là \(a = \frac{1}{2}\)
Video hướng dẫn giải
Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là 3 và cắt trục tung tại điểm có tung độ bằng -1
Phương pháp giải:
Xác định a , b của hàm số bậc nhất \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Hàm số có hệ số góc bằng 3 nên hàm số bậc nhất cần tìm là: y = 3x + b
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng -1 nên ta thay điểm (0; -1) vào công thức hàm số y = 3x + b ta được: b = -1
Vậy hàm số bậc nhất đó là: y=3x−1
Video hướng dẫn giải
Đường thẳng \(y = \frac{{2{\rm{x}} + 1}}{2}\) có hệ số góc bằng bao nhiêu?
Tròn: Đường thẳng này có hệ số góc a = 2
Vuông: Không đúng, đường thẳng này có hệ số góc a = 1
Theo em, bạn nào trả lời đúng, bạn nào trả lời sai? Vì sao?
Phương pháp giải:
Biến đổi hàm số \(y = \frac{{2{\rm{x}} + 1}}{2} = \frac{{2{\rm{x}}}}{2} + \frac{1}{2} = x + \frac{1}{2}\) từ đó xác định được hệ số góc và tìm ra được bạn nào đúng, bạn nào sai.
Lời giải chi tiết:
Ta có: \(y = \frac{{2{\rm{x}} + 1}}{2} = \frac{{2{\rm{x}}}}{2} + \frac{1}{2} = x + \frac{1}{2}\)
Hệ số góc của đường thẳng \(y = \frac{{2{\rm{x}} + 1}}{2}\) là \(a = 1\).
Như vậy bạn tròn sai và bạn vuông đúng.
Mục 1 trang 51, 52 SGK Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với phân thức đại số. Đây là nền tảng quan trọng để học sinh tiếp cận các bài toán phức tạp hơn trong chương trình học.
Mục 1 yêu cầu học sinh thực hành các kỹ năng sau:
Để giải các bài tập trong Mục 1 trang 51, 52 SGK Toán 8 tập 2 - Kết nối tri thức một cách hiệu quả, học sinh cần nắm vững các bước sau:
a) (x^2 - 4)/(x + 2)
Lời giải:
(x^2 - 4)/(x + 2) = ((x - 2)(x + 2))/(x + 2) = x - 2 (với x ≠ -2)
b) (x^2 + 2x + 1)/(x + 1)
Lời giải:
(x^2 + 2x + 1)/(x + 1) = ((x + 1)^2)/(x + 1) = x + 1 (với x ≠ -1)
a) 1/2 và 2/3
Lời giải:
MTC = 6
1/2 = 3/6 và 2/3 = 4/6
b) x/2x + 1 và 1/x
Lời giải:
MTC = x(2x + 1)
x/2x + 1 = x^2/x(2x + 1) và 1/x = (2x + 1)/x(2x + 1)
a) 1/x + 2/x
Lời giải:
1/x + 2/x = (1 + 2)/x = 3/x
b) (x + 1)/2 - (x - 1)/2
Lời giải:
(x + 1)/2 - (x - 1)/2 = (x + 1 - (x - 1))/2 = (x + 1 - x + 1)/2 = 2/2 = 1
Để nắm vững kiến thức về phân thức đại số và các phép toán với phân thức, học sinh nên luyện tập thêm các bài tập trong sách bài tập và các đề thi thử. Ngoài ra, việc tìm hiểu các tài liệu tham khảo khác cũng sẽ giúp học sinh hiểu sâu hơn về chủ đề này.
Mục 1 trang 51, 52 SGK Toán 8 tập 2 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 8. Việc nắm vững kiến thức và kỹ năng trong mục này sẽ giúp học sinh tự tin giải các bài toán phức tạp hơn và đạt kết quả tốt trong các kỳ thi.