Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 98, 99, 100 sách giáo khoa Toán 8 tập 2 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
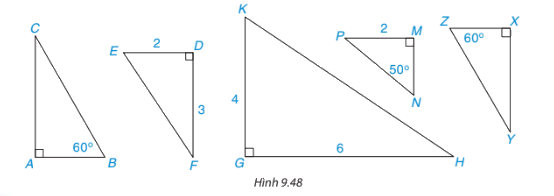
Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:
Video hướng dẫn giải
Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:
Phương pháp giải:
Sử dụng các trường hợp đồng dạng của tam giác.
Lời giải chi tiết:
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{{D}}F \backsim \Delta KGH\left( {\frac{{E{{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{{D}}F} = \widehat {KGH}} \right)\end{array}\)
Video hướng dẫn giải
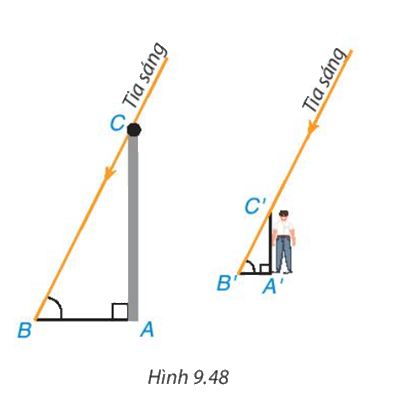
Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6m và bóng của Việt dài 70cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy" Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được.
Ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai canh góc vuông của tam giác A'B'C' vuông tại đỉnh A'. Vì các tia sáng mặt trời tạo với hai cái bóng các góc bằng nhau nên \(\widehat B = \widehat {B'}\)
a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?
b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?
Phương pháp giải:
Chứng minh ΔABC ∽ ΔA′B′C′ suy ra các tỉ số đồng dạng và tính AC
Lời giải chi tiết:
a) Hai tam giác vuông ABC và A'B'C' có \(\widehat B = \widehat {B'}\)
=> ΔABC ∽ ΔA′B′C′
b) Vì ΔABC ∽ ΔA′B′C′ nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
hay \(\frac{{0,7}}{6} = \frac{{1,4}}{{AC}}\) suy ra AC=12(m)
Video hướng dẫn giải
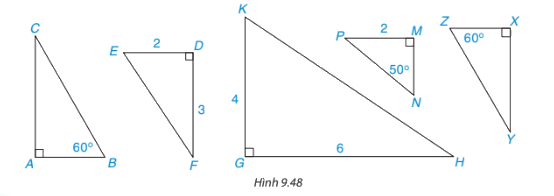
Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48:
Phương pháp giải:
Sử dụng các trường hợp đồng dạng của tam giác.
Lời giải chi tiết:
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{{D}}F \backsim \Delta KGH\left( {\frac{{E{{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{{D}}F} = \widehat {KGH}} \right)\end{array}\)
Video hướng dẫn giải
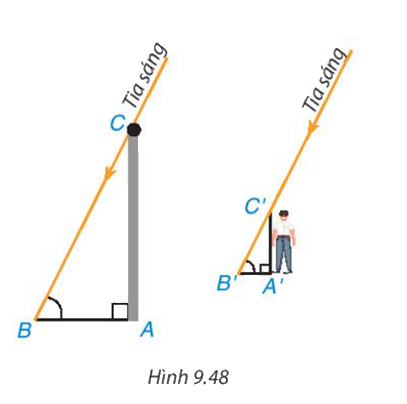
Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6m và bóng của Việt dài 70cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4m. Nam liền reo lên: "Tớ biết cột cờ cao bao nhiêu rồi đấy" Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được.
Ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai canh góc vuông của tam giác A'B'C' vuông tại đỉnh A'. Vì các tia sáng mặt trời tạo với hai cái bóng các góc bằng nhau nên \(\widehat B = \widehat {B'}\)
a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?
b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AC như thế nào và kết quả là bao nhiêu?
Phương pháp giải:
Chứng minh ΔABC ∽ ΔA′B′C′ suy ra các tỉ số đồng dạng và tính AC
Lời giải chi tiết:
a) Hai tam giác vuông ABC và A'B'C' có \(\widehat B = \widehat {B'}\)
=> ΔABC ∽ ΔA′B′C′
b) Vì ΔABC ∽ ΔA′B′C′ nên \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
hay \(\frac{{0,7}}{6} = \frac{{1,4}}{{AC}}\) suy ra AC=12(m)
Video hướng dẫn giải
Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chấn đến mắt người ấy là 1,6m(H9.51)
A: Vị trí đỉnh cây
B: Vị trí gốc cây
C: Vị trí đỉnh cột.
D: Vị trí mắt
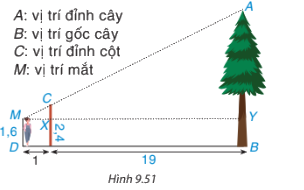
Phương pháp giải:
Chứng minh tam giác MXC đồng dạng với tam giác MYA rồi suy ra các tỉ số đồng dạng. Tính được chiều cao của cây.
Lời giải chi tiết:
Ta có: CX = 2,4 – 1,6 = 0,8(m)
MY = 1 + 19 = 20 (m)
Xét tam giác MXC và tam giác MYA có: góc M chung; \(\widehat {M{{X}}C} = \widehat {MY{{A}}}\)
nên \( \Delta M{{X}}C \backsim \Delta MY{{A}}\)
suy ra \(\frac{{M{{X}}}}{{MY}} = \frac{{XC}}{{Y{{A}}}}\)
hay \(\frac{1}{{20}} = \frac{{0,8}}{{Y{{A}}}}\)
nên \(Y{{A}} = 20.0,8 = 16(m)\)
Vậy chiều cao của cây là: \(AB = BY + Y{{A}} = 1,6 + 16 = 17,6(m)\)
Video hướng dẫn giải
Một người đo chiều cao của một cái cây bằng cách cắm một chiếc cọc xuống đất, cọc cao 2,4m và cách vị trí gốc cây 19m. Người đo đứng cách xa chiếc cọc 1m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chấn đến mắt người ấy là 1,6m(H9.51)
A: Vị trí đỉnh cây
B: Vị trí gốc cây
C: Vị trí đỉnh cột.
D: Vị trí mắt
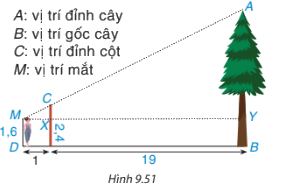
Phương pháp giải:
Chứng minh tam giác MXC đồng dạng với tam giác MYA rồi suy ra các tỉ số đồng dạng. Tính được chiều cao của cây.
Lời giải chi tiết:
Ta có: CX = 2,4 – 1,6 = 0,8(m)
MY = 1 + 19 = 20 (m)
Xét tam giác MXC và tam giác MYA có: góc M chung; \(\widehat {M{{X}}C} = \widehat {MY{{A}}}\)
nên \( \Delta M{{X}}C \backsim \Delta MY{{A}}\)
suy ra \(\frac{{M{{X}}}}{{MY}} = \frac{{XC}}{{Y{{A}}}}\)
hay \(\frac{1}{{20}} = \frac{{0,8}}{{Y{{A}}}}\)
nên \(Y{{A}} = 20.0,8 = 16(m)\)
Vậy chiều cao của cây là: \(AB = BY + Y{{A}} = 1,6 + 16 = 17,6(m)\)
Mục 1 của chương trình Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tứ giác. Các bài tập trong trang 98, 99, 100 SGK Toán 8 tập 2 yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tứ giác, đặc biệt là hình thang cân.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và tự luận về các khái niệm cơ bản của tứ giác như định nghĩa, các loại tứ giác (hình chữ nhật, hình thoi, hình vuông, hình bình hành, hình thang, hình thang cân), các tính chất của các loại tứ giác này.
Bài 2 tập trung vào việc nghiên cứu sâu hơn về hình thang cân, bao gồm các định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân. Các bài tập thường yêu cầu học sinh:
Bài 3 giới thiệu về đường trung bình của tam giác và đường trung bình của hình thang, các tính chất và ứng dụng của chúng. Các bài tập thường yêu cầu học sinh:
Ví dụ: Cho hình thang cân ABCD (AB // CD), AB = 5cm, CD = 10cm, AD = 6cm. Tính độ dài đường cao của hình thang.
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Ta có: DH = KC = (CD - AB) / 2 = (10 - 5) / 2 = 2.5cm.
Áp dụng định lý Pitago vào tam giác ADH, ta có: AH2 = AD2 - DH2 = 62 - 2.52 = 36 - 6.25 = 29.75.
Suy ra: AH = √29.75 ≈ 5.45cm.
Vậy, đường cao của hình thang là 5.45cm.
Để học tốt môn Toán 8, các em cần thường xuyên luyện tập, làm bài tập đầy đủ và nắm vững kiến thức lý thuyết. Ngoài ra, các em có thể tham khảo các tài liệu tham khảo, các trang web học toán online để bổ sung kiến thức và rèn luyện kỹ năng.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập Toán 8 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!