Bài 9.26 trang 103 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.26, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn
Đề bài
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC=3AB, B′D′=3A′B′
a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'
b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2m2 thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh ΔABC \( \backsim \) ΔC′D′B′ và ΔC′D′B′=ΔA′B′C′ suy ra ΔABC\( \backsim \) ΔA′B′C′
b) Xét tỉ lệ hai tam giác ABCD và A'B'C'D', có
\(\frac{{AB.BC}}{{A'B'.B'C'}} = \frac{{AB}}{{A'B'}}.\frac{{BC}}{{B'C'}} = \frac{1}{4}\)
Suy ra diện tích hình chữ nhật A'B'C'D'
Lời giải chi tiết
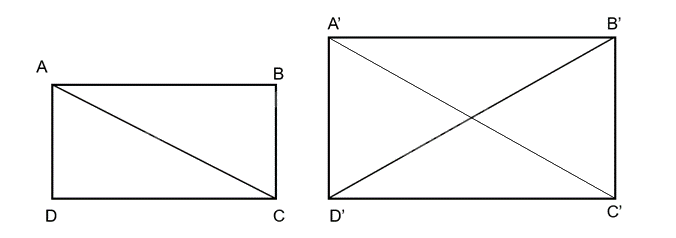
a) Ta có: AC=3AB nên \(\frac{{AB}}{{AC}} = \frac{1}{3}\)
Ta có: B′D′=3A′B′ nên \(\frac{{A'B'}}{{B'D'}} = \frac{1}{3}\)
Suy ra \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)
Xét tam giác vuông ABC (vuông tại B) và tam giác vuông B'A'D' (vuông tại A') có:
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)
\(\widehat{BAC} = \widehat{B'A'D'}\)
nên ΔABC \( \backsim \) ΔA'B'D' (1)
- Xét ΔB'A'D' và ΔA′B′C′ có:
A'B' chung
A′B′ = C′D′ (A'B'C'D là hình chữ nhật)
B′D′ = A′C′(hai hình chéo của chữ nhật)
nên ΔB'A'D'=ΔA′B′C′ (2)
Từ (1) và (2) suy ra ΔABC \( \backsim \) ΔA′B′C′
b) - Vì A′B′=2AB nên \(\frac{{AB}}{{A'B'}} = \frac{1}{2}\)
mà ΔABC ∽ ΔA'B'C' nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)
Diện tích ABCD là: AB.BC
Diện tích A'B'C'D' là: A′B′.B′C′
Xét tỉ lệ hai hình chữ nhật ABCD và A'B'C'D', có
\(\frac{S_{ABCD}}{S_{A′B′C′D′}}\frac{{AB.BC}}{{A'B'.B'C'}} = \frac{{AB}}{{A'B'}}.\frac{{BC}}{{B'C'}} = \frac{1}{2} . \frac{1}{2} = \frac{1}{4}\)
Do đó \(S_{A′B′C′D′}=4S_{ABCD}\)
mà \(S_{ABCD}=2m^2\) nên \(S_{A′B′C′D′}=4.2 = 8(m^2)\)
Bài 9.26 SGK Toán 8 tập 2 Kết nối tri thức là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật.
Một hình hộp chữ nhật có chiều dài 12cm, chiều rộng 5cm và chiều cao 8cm. Tính:
Để giải bài toán này, chúng ta cần nhớ lại các công thức sau:
Áp dụng các công thức trên, ta có:
Diện tích xung quanh = 2(12 + 5) x 8 = 2 x 17 x 8 = 272 (cm2)
Diện tích toàn phần = 2(12 x 5 + 12 x 8 + 5 x 8) = 2(60 + 96 + 40) = 2 x 196 = 392 (cm2)
Thể tích = 12 x 5 x 8 = 480 (cm3)
Trong quá trình giải bài toán, điều quan trọng là phải xác định đúng các kích thước của hình hộp chữ nhật (dài, rộng, cao) và áp dụng đúng công thức. Việc hiểu rõ ý nghĩa của từng công thức sẽ giúp học sinh giải quyết các bài toán tương tự một cách dễ dàng hơn.
Ví dụ, diện tích xung quanh của hình hộp chữ nhật chính là tổng diện tích của bốn mặt bên. Diện tích toàn phần bao gồm diện tích xung quanh và diện tích của hai đáy. Thể tích của hình hộp chữ nhật cho biết không gian mà hình hộp chữ nhật chiếm giữ.
Để củng cố kiến thức về hình hộp chữ nhật, các em có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài 9.26 trang 103 SGK Toán 8 tập 2 - Kết nối tri thức và có thể tự tin giải các bài tập tương tự. Chúc các em học tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.