Bài 3.23 trang 63 SGK Toán 8 tập 1 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.23 trang 63 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Cho hình bình hành ABCD.
Đề bài
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a. Chứng minh tứ giác AEFD, ABFC có cặp cạnh đối song song và bằng nhau nên các tứ giác AEFD, ABFC là hình bình hành.
b. Sử dụng tính chất đường chéo của hình bình hành với hình bình hành AEFD và ABFC để chứng minh.
Lời giải chi tiết
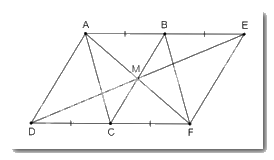
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.
Mà hai điểm B, C lần lượt là trung điểm AE, DF.
Suy ra AE = DF; AB = BE = CD = CF.
Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).
Do đó tứ giác AEFD là hình bình hành.
Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).
Do đó tứ giác ABFC là hình bình hành.
Vậy ta chứng minh được hai tứ giác AEFD, ABFC là những hình bình hành.
b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là M.
Hình bình hành AEFD có hai đường chéo AF và BC.
Mà M là trung điểm của AF.
Suy ra M cũng là trung điểm của BC.
Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
Bài 3.23 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của các góc so le trong, đồng vị, trong cùng phía.
Cho hình vẽ sau (hình vẽ minh họa bài 3.23 SGK Toán 8 tập 1 - Kết nối tri thức). Biết rằng a // b. Tìm số đo của các góc còn lại trên hình.
Để giải bài tập này, chúng ta sẽ sử dụng các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song:
Bước 1: Xác định các góc đã biết.
Giả sử góc A1 = 60 độ (ví dụ). Từ đó, ta có thể suy ra các góc khác.
Bước 2: Sử dụng tính chất góc so le trong.
Nếu góc A1 và góc B1 là góc so le trong, thì góc B1 = góc A1 = 60 độ.
Bước 3: Sử dụng tính chất góc đồng vị.
Nếu góc A1 và góc B2 là góc đồng vị, thì góc B2 = góc A1 = 60 độ.
Bước 4: Sử dụng tính chất góc trong cùng phía.
Nếu góc A1 và góc B3 là góc trong cùng phía, thì góc A1 + góc B3 = 180 độ. Suy ra, góc B3 = 180 độ - góc A1 = 180 độ - 60 độ = 120 độ.
Bước 5: Tiếp tục suy luận để tìm các góc còn lại.
Sử dụng các tính chất trên, ta có thể suy ra các góc còn lại trên hình.
Giả sử góc A1 = 70 độ. Hãy tìm các góc còn lại.
Khi giải bài tập này, học sinh cần vẽ hình chính xác và chú ý đến các góc đã biết để suy luận ra các góc còn lại. Việc hiểu rõ các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song là rất quan trọng.
Để rèn luyện kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 8 tập 1 - Kết nối tri thức.
Bài 3.23 trang 63 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ nắm vững kiến thức và giải bài tập một cách hiệu quả.