Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết các bài tập trang 15 và 16 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất bài toán, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hai đa thức:
Video hướng dẫn giải
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu
\(A - B = \left( {5{x^2}y + 5x - 3} \right) - \left( {xy - 4{x^2}y + 5x - 1} \right)\), bỏ dấu ngoặc rồi thu gọn đa thức nhận được.
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}A - B = \left( {5{x^2}y + 5x - 3} \right) - \left( {xy - 4{x^2}y + 5x - 1} \right)\\ = 5{x^2}y + 5x - 3 - xy + 4{x^2}y - 5x + 1\\ = \left( {5{x^2}y + 4{x^2}y} \right) - xy + \left( {5x + 5x} \right) + \left( { - 3 + 1} \right)\\ = 9{x^2}y - xy + 10x - 2\end{array}\)
Video hướng dẫn giải
Thực hiện phép cộng hai đa thức A và B bằng cách tiến hành các bước sau:
Phương pháp giải:
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}A + B = \left( {5{x^2}y + 5x - 3} \right) + \left( {xy - 4{x^2}y + 5x - 1} \right)\\ = 5{x^2}y + 5x - 3 + xy - 4{x^2}y + 5x - 1\\ = \left( {5{x^2}y - 4{x^2}y} \right) + xy + \left( {5x + 5x} \right) + \left( { - 3 - 1} \right)\\ = {x^2}y + xy + 10x - 4\end{array}\)
Video hướng dẫn giải
Cho hai đa thức \(G = {x^2}y - 3xy - 3\) và \(H = 3{x^2}y + xy - 0,5x + 5\).
Hãy tính G+H và G-H.
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}G + H = \left( {{x^2}y - 3xy - 3} \right) + \left( {3{x^2}y + xy - 0,5x + 5} \right)\\ = {x^2}y - 3xy - 3 + 3{x^2}y + xy - 0,5x + 5\\ = \left( {{x^2}y + 3{x^2}y} \right) + \left( { - 3xy + xy} \right) - 0,5x + \left( { - 3 + 5} \right)\\ = 4{x^2}y - 2xy - 0,5x + 2.\\G - H = \left( {{x^2}y - 3xy - 3} \right) - \left( {3{x^2}y + xy - 0,5x + 5} \right)\\ = {x^2}y - 3xy - 3 - 3{x^2}y - xy + 0,5x - 5\\ = \left( {{x^2}y - 3{x^2}y} \right) + \left( { - 3xy - xy} \right) + 0,5x + \left( { - 3 - 5} \right)\\ = - 2{x^2}y - 4xy + 0,5x - 8.\end{array}\)
Video hướng dẫn giải
Rút gọn và tính giá trị của biểu thức sau tại x=2 và y=-1.
\(K = \left( {{x^2}y + 2x{y^3}} \right) - \left( {7,5{x^3}{y^2} - {x^3}} \right) + \left( {3x{y^3} - {x^2}y + 7,5{x^3}{y^2}} \right)\)
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Thay x=2 và y=-1 vào biểu thức rồi tính giá trị biểu thức.
Lời giải chi tiết:
\(\begin{array}{l}K = \left( {{x^2}y + 2x{y^3}} \right) - \left( {7,5{x^3}{y^2} - {x^3}} \right) + \left( {3x{y^3} - {x^2}y + 7,5{x^3}{y^2}} \right)\\ = {x^2}y + 2x{y^3} - 7,5{x^3}{y^2} + {x^3} + 3x{y^3} - {x^2}y + 7,5{x^3}{y^2}\\ = \left( {{x^2}y - {x^2}y} \right) + \left( {2x{y^3} + 3x{y^3}} \right) + \left( { - 7,5{x^3}{y^2} + 7,5{x^3}{y^2}} \right) + {x^3}\\ = 5x{y^3} + {x^3}\end{array}\)
Thay x=2, y=-1 vào K ta được \(K = 5.2.{\left( { - 1} \right)^3} + {2^3} = - 10 + 8 = - 2.\)
Cho hai đa thức:
\(A = 5{x^2}y + 5x - 3\) và \(B = xy - 4{x^2}y + 5x - 1\).
Video hướng dẫn giải
Thực hiện phép cộng hai đa thức A và B bằng cách tiến hành các bước sau:
Phương pháp giải:
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}A + B = \left( {5{x^2}y + 5x - 3} \right) + \left( {xy - 4{x^2}y + 5x - 1} \right)\\ = 5{x^2}y + 5x - 3 + xy - 4{x^2}y + 5x - 1\\ = \left( {5{x^2}y - 4{x^2}y} \right) + xy + \left( {5x + 5x} \right) + \left( { - 3 - 1} \right)\\ = {x^2}y + xy + 10x - 4\end{array}\)
Video hướng dẫn giải
Thực hiện phép trừ hai đa thức A và B bằng cách lập hiệu
\(A - B = \left( {5{x^2}y + 5x - 3} \right) - \left( {xy - 4{x^2}y + 5x - 1} \right)\), bỏ dấu ngoặc rồi thu gọn đa thức nhận được.
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}A - B = \left( {5{x^2}y + 5x - 3} \right) - \left( {xy - 4{x^2}y + 5x - 1} \right)\\ = 5{x^2}y + 5x - 3 - xy + 4{x^2}y - 5x + 1\\ = \left( {5{x^2}y + 4{x^2}y} \right) - xy + \left( {5x + 5x} \right) + \left( { - 3 + 1} \right)\\ = 9{x^2}y - xy + 10x - 2\end{array}\)
Video hướng dẫn giải
Cho hai đa thức \(G = {x^2}y - 3xy - 3\) và \(H = 3{x^2}y + xy - 0,5x + 5\).
Hãy tính G+H và G-H.
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Lời giải chi tiết:
\(\begin{array}{l}G + H = \left( {{x^2}y - 3xy - 3} \right) + \left( {3{x^2}y + xy - 0,5x + 5} \right)\\ = {x^2}y - 3xy - 3 + 3{x^2}y + xy - 0,5x + 5\\ = \left( {{x^2}y + 3{x^2}y} \right) + \left( { - 3xy + xy} \right) - 0,5x + \left( { - 3 + 5} \right)\\ = 4{x^2}y - 2xy - 0,5x + 2.\\G - H = \left( {{x^2}y - 3xy - 3} \right) - \left( {3{x^2}y + xy - 0,5x + 5} \right)\\ = {x^2}y - 3xy - 3 - 3{x^2}y - xy + 0,5x - 5\\ = \left( {{x^2}y - 3{x^2}y} \right) + \left( { - 3xy - xy} \right) + 0,5x + \left( { - 3 - 5} \right)\\ = - 2{x^2}y - 4xy + 0,5x - 8.\end{array}\)
Video hướng dẫn giải
Rút gọn và tính giá trị của biểu thức sau tại x=2 và y=-1.
\(K = \left( {{x^2}y + 2x{y^3}} \right) - \left( {7,5{x^3}{y^2} - {x^3}} \right) + \left( {3x{y^3} - {x^2}y + 7,5{x^3}{y^2}} \right)\)
Phương pháp giải:
Phá ngoặc, chú ý trước dấu ngoặc là dấu (-) nên khi phá ngoặc, ta đổi dấu tất cả các hạng tử trong dấu ngoặc.
Sử dụng tính chất giao hoán, kết hợp các hạng tử đồng dạng với nhau rồi thu gọn.
Thay x=2 và y=-1 vào biểu thức rồi tính giá trị biểu thức.
Lời giải chi tiết:
\(\begin{array}{l}K = \left( {{x^2}y + 2x{y^3}} \right) - \left( {7,5{x^3}{y^2} - {x^3}} \right) + \left( {3x{y^3} - {x^2}y + 7,5{x^3}{y^2}} \right)\\ = {x^2}y + 2x{y^3} - 7,5{x^3}{y^2} + {x^3} + 3x{y^3} - {x^2}y + 7,5{x^3}{y^2}\\ = \left( {{x^2}y - {x^2}y} \right) + \left( {2x{y^3} + 3x{y^3}} \right) + \left( { - 7,5{x^3}{y^2} + 7,5{x^3}{y^2}} \right) + {x^3}\\ = 5x{y^3} + {x^3}\end{array}\)
Thay x=2, y=-1 vào K ta được \(K = 5.2.{\left( { - 1} \right)^3} + {2^3} = - 10 + 8 = - 2.\)
Video hướng dẫn giải
Trở lại tình huống mở đầu, hãy trình bày ý kiến của em.
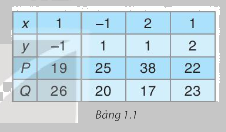
Trong buổi sinh hoạt câu lạc bộ Toán học của lớp, hai bạn tính giá trị của đa thức \(P = 2{x^2}y - x{y^2} + 22\) và \(Q = x{y^2} - 2{x^2}y + 23\) tại những giá trị cho trước của x và y. Kết quả được ghi lại như bảng bên.
Ban giám khảo cho biết có một cột cho kết quả sai.
Theo em, làm thế nào để có thể nhanh chóng phát hiện cột có kết quả sai ấy?
Phương pháp giải:
Phát hiện tính chất của tổng P+Q.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}P + Q = \left( {2{x^2}y - x{y^2} + 22} \right) + \left( {x{y^2} - 2{x^2}y + 23} \right)\\ = 2{x^2}y - x{y^2} + 22 + x{y^2} - 2{x^2}y + 23\\ = \left( {2{x^2}y - 2{x^2}y} \right) + \left( { - x{y^2} + x{y^2}} \right) + \left( {22 + 23} \right)\\ = 45.\end{array}\)
Quan sát cột có tổng P+Q khác 45 thì cột đó có kết quả sai.
Như vậy cột 3 có kết quả sai.
Video hướng dẫn giải
Trở lại tình huống mở đầu, hãy trình bày ý kiến của em.
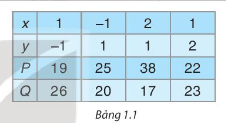
Trong buổi sinh hoạt câu lạc bộ Toán học của lớp, hai bạn tính giá trị của đa thức \(P = 2{x^2}y - x{y^2} + 22\) và \(Q = x{y^2} - 2{x^2}y + 23\) tại những giá trị cho trước của x và y. Kết quả được ghi lại như bảng bên.
Ban giám khảo cho biết có một cột cho kết quả sai.
Theo em, làm thế nào để có thể nhanh chóng phát hiện cột có kết quả sai ấy?
Phương pháp giải:
Phát hiện tính chất của tổng P+Q.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}P + Q = \left( {2{x^2}y - x{y^2} + 22} \right) + \left( {x{y^2} - 2{x^2}y + 23} \right)\\ = 2{x^2}y - x{y^2} + 22 + x{y^2} - 2{x^2}y + 23\\ = \left( {2{x^2}y - 2{x^2}y} \right) + \left( { - x{y^2} + x{y^2}} \right) + \left( {22 + 23} \right)\\ = 45.\end{array}\)
Quan sát cột có tổng P+Q khác 45 thì cột đó có kết quả sai.
Như vậy cột 3 có kết quả sai.
Chương trình Toán 8 tập 1 Kết nối tri thức tập trung vào việc xây dựng nền tảng vững chắc về đại số và hình học. Trang 15 và 16 của sách giáo khoa chứa đựng những bài tập quan trọng, giúp học sinh củng cố kiến thức về các phép toán, biểu thức đại số và các tính chất cơ bản của hình học.
Bài 1 yêu cầu học sinh thu gọn các biểu thức đại số cho trước. Để giải bài này, học sinh cần nắm vững các quy tắc về phép cộng, trừ, nhân, chia các đơn thức và đa thức. Ví dụ, để thu gọn biểu thức 3x + 2x - 5x, ta thực hiện phép cộng và trừ các hệ số của x, kết quả là 0x hay đơn giản là 0.
Bài 2 yêu cầu học sinh tìm giá trị của biểu thức khi biết giá trị của các biến. Để giải bài này, học sinh cần thay thế các giá trị của biến vào biểu thức và thực hiện các phép toán để tìm ra kết quả. Ví dụ, nếu biểu thức là 2x + 3y và x = 1, y = 2, thì giá trị của biểu thức là 2(1) + 3(2) = 2 + 6 = 8.
Bài 3 giới thiệu cho học sinh về phương trình đơn giản và cách giải phương trình. Phương trình là một đẳng thức chứa biến. Để giải phương trình, ta cần tìm giá trị của biến sao cho đẳng thức được thỏa mãn. Ví dụ, phương trình 2x + 1 = 5 có nghiệm là x = 2, vì khi thay x = 2 vào phương trình, ta có 2(2) + 1 = 5, là một đẳng thức đúng.
Bài 4 thường là các bài toán ứng dụng kiến thức đã học vào các tình huống thực tế. Các bài toán này giúp học sinh hiểu rõ hơn về ý nghĩa và tầm quan trọng của toán học trong cuộc sống. Ví dụ, một bài toán có thể yêu cầu tính diện tích của một mảnh đất hình chữ nhật, hoặc tính số tiền lãi khi gửi tiết kiệm.
Dưới đây là lời giải chi tiết cho từng bài tập trong trang 15 và 16 SGK Toán 8 tập 1 Kết nối tri thức:
Để học tốt môn Toán 8, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập trang 15, 16 SGK Toán 8 tập 1 Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán 8. Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập và đạt kết quả tốt nhất.