Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tại giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 83, 84, 85 sách giáo khoa Toán 8 tập 2 - Kết nối tri thức.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp cho các em những phương pháp giải bài tập hiệu quả nhất, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Cho hai tam giác ABC và A'B'C' có
Video hướng dẫn giải
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh ΔABC ∽ ΔDEF
Phương pháp giải:
Chứng minh : \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\) từ đó suy ra: ΔABC ∽ ΔDEF
Lời giải chi tiết:
Vì chu vi tam giác ABC bằng 18cm
=> AB+AC+BC=18 => 4+AC+6=18 => AC=8 (cm)
Vì chu vi tam giác DEF bằng 27cm
=> DE+EF+DF=27 => 6+EF+12=27 => EF=9 (cm)
Ta thấy \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\\ = \frac{4}{6} = \frac{8}{{12}} = \frac{6}{9} = \frac{2}{3}\end{array}\)
=> ΔABC ∽ ΔDEF
Video hướng dẫn giải
Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.
Phương pháp giải:
Vẽ tam giác dựa vào tỉ lệ của độ rộng khung thành và khoảng cách của trái bóng với hai cột gôn.
Lời giải chi tiết:
Ta có tỉ lệ của độ rộng khung thành và khoảng cách hai cột gôn là: 7,32 : 10,98 : 14,64 = 2 : 3 : 4 nên độ dài cạnh của tam giác vẽ theo tỉ lệ 2 : 3 : 4.
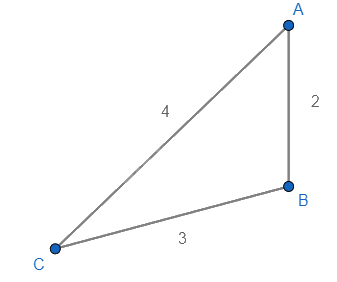
Sử dụng thước đo góc, ta được \( \widehat C \approx 29^0 \) hay góc sút bằng khoảng \(29^0\).
Video hướng dẫn giải
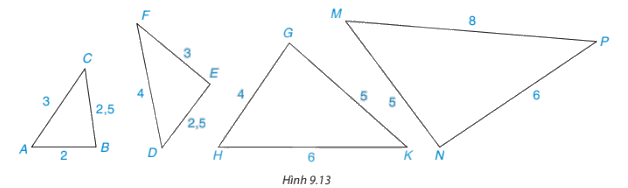
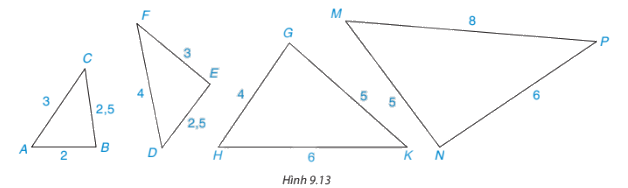
Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Phương pháp giải:
Tính tỉ lệ giữa các cạnh của tam giác.
Lời giải chi tiết:
Các cặp tam giác đồng dạng là: \(\Delta ABC \backsim \Delta HKG{;^{}}\Delta EFD \backsim \Delta NPM\)
Video hướng dẫn giải
Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
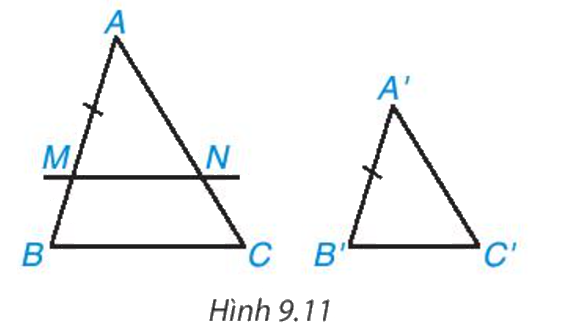
b) Nếu A′B < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Phương pháp giải:
Sử dụng hai tam giác đồng dạng để chứng minh các yêu cầu của bài toán.
Lời giải chi tiết:
a) Nếu A′B′=AB thì tam giác có đồng dạng.
Vì A′B′=AB \( \Rightarrow \)A’C’=AC => B’C’=BC => \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
=> Hai tam giác đồng dạng
b) MN // BC ( M∈AB, N∈AC) => ΔAMN ∽ ΔABC
=> \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
=> \(\frac{{A'B'}}{{AM}} = \frac{{A'C'}}{{AN}} = \frac{{B'C'}}{{MN}}\)
- Có AM= A’B’ => A’C’=AN \( \Rightarrow \) B’C’=MN
=> ΔAMN = ΔA'B'C'
=> ΔAMN ∽ ΔA'B'C'
Mà ΔAMN ∽ ΔABC
=> ΔABC ∽ ΔA′B′C′
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC. Vì \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
Video hướng dẫn giải
Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
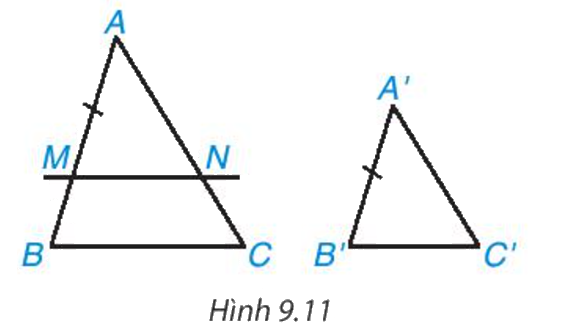
b) Nếu A′B < AB như hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A'B'. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Phương pháp giải:
Sử dụng hai tam giác đồng dạng để chứng minh các yêu cầu của bài toán.
Lời giải chi tiết:
a) Nếu A′B′=AB thì tam giác có đồng dạng.
Vì A′B′=AB \( \Rightarrow \)A’C’=AC => B’C’=BC => \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
=> Hai tam giác đồng dạng
b) MN // BC ( M∈AB, N∈AC) => ΔAMN ∽ ΔABC
=> \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
=> \(\frac{{A'B'}}{{AM}} = \frac{{A'C'}}{{AN}} = \frac{{B'C'}}{{MN}}\)
- Có AM= A’B’ => A’C’=AN \( \Rightarrow \) B’C’=MN
=> ΔAMN = ΔA'B'C'
=> ΔAMN ∽ ΔA'B'C'
Mà ΔAMN ∽ ΔABC
=> ΔABC ∽ ΔA′B′C′
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC. Vì \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
Video hướng dẫn giải
Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Phương pháp giải:
Tính tỉ lệ giữa các cạnh của tam giác.
Lời giải chi tiết:
Các cặp tam giác đồng dạng là: \(\Delta ABC \backsim \Delta HKG{;^{}}\Delta EFD \backsim \Delta NPM\)
Video hướng dẫn giải
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh ΔABC ∽ ΔDEF
Phương pháp giải:
Chứng minh : \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\) từ đó suy ra: ΔABC ∽ ΔDEF
Lời giải chi tiết:
Vì chu vi tam giác ABC bằng 18cm
=> AB+AC+BC=18 => 4+AC+6=18 => AC=8 (cm)
Vì chu vi tam giác DEF bằng 27cm
=> DE+EF+DF=27 => 6+EF+12=27 => EF=9 (cm)
Ta thấy \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\\ = \frac{4}{6} = \frac{8}{{12}} = \frac{6}{9} = \frac{2}{3}\end{array}\)
=> ΔABC ∽ ΔDEF
Video hướng dẫn giải
Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.
Phương pháp giải:
Vẽ tam giác dựa vào tỉ lệ của độ rộng khung thành và khoảng cách của trái bóng với hai cột gôn.
Lời giải chi tiết:
Ta có tỉ lệ của độ rộng khung thành và khoảng cách hai cột gôn là: 7,32 : 10,98 : 14,64 = 2 : 3 : 4 nên độ dài cạnh của tam giác vẽ theo tỉ lệ 2 : 3 : 4.
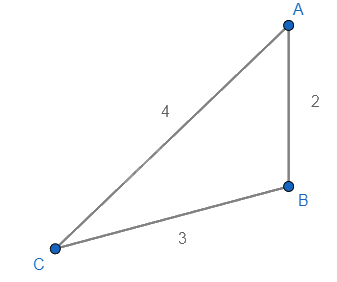
Sử dụng thước đo góc, ta được \( \widehat C \approx 29^0 \) hay góc sút bằng khoảng \(29^0\).
Mục 1 của chương trình Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập và hệ thống hóa các kiến thức về tứ giác. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán thực tế liên quan đến tứ giác, đặc biệt là hình thang cân.
Bài 1 yêu cầu học sinh nhắc lại các định nghĩa, tính chất của các loại tứ giác đã học (hình bình hành, hình chữ nhật, hình thoi, hình vuông, hình thang). Đồng thời, học sinh cần biết cách áp dụng các tính chất này để chứng minh một tứ giác là một loại tứ giác cụ thể.
Bài 2 tập trung vào việc ôn tập và củng cố kiến thức về hình thang cân. Học sinh cần nắm vững các tính chất đặc trưng của hình thang cân, như hai cạnh đáy song song, hai cạnh bên bằng nhau, hai góc kề một cạnh bên bằng nhau, và hai đường chéo bằng nhau.
Bài 3 là một bài tập vận dụng tổng hợp, yêu cầu học sinh áp dụng các kiến thức đã học về tứ giác và hình thang cân để giải quyết một bài toán thực tế. Bài toán này thường liên quan đến việc tính toán diện tích, chu vi, hoặc chứng minh một tính chất nào đó của hình.
Để giải các bài tập trong mục 1 trang 83, 84, 85 SGK Toán 8 tập 2 - Kết nối tri thức một cách hiệu quả, học sinh cần:
Ngoài việc giải các bài tập trong SGK, học sinh nên làm thêm các bài tập nâng cao để rèn luyện kỹ năng và mở rộng kiến thức. Các em cũng có thể tham khảo các tài liệu tham khảo, các trang web học toán online để tìm hiểu thêm về các kiến thức liên quan.
| Công thức | Mô tả |
|---|---|
| Diện tích hình thang | S = (a + b)h/2 (a, b là độ dài hai đáy, h là chiều cao) |
| Đường trung bình của hình thang | m = (a + b)/2 (a, b là độ dài hai đáy) |
Hy vọng với những hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải các bài tập Toán 8 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!