Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 2 - Kết nối tri thức. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những em học sinh mới làm quen với chương trình.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc
Video hướng dẫn giải
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB=13m, A′B′=6,5m và độ cao lần lượt là BH=5m, B′H′=2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'
- Nhận xét về hai đại lượng \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}}\)
- Dùng định lí Pythagore để tính AH và A'H'
- So sánh các đại lượng \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}}\)
- Hai tam giác vuông A'H'B' và AHB có đồng dạng không
Phương pháp giải:
- Tính các tỉ số theo yêu cầu của bài toán dựa vào độ dài đã biết.
Lời giải chi tiết:
- Có \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
- Áp dụng định lý Pythagore có \(AH = 12 ;A'H' = 6 \)
- Có \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
=> Hai tam giác vuông A'H'B' và AHB đồng dạng
Video hướng dẫn giải
Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không? (Biết rằng 1 inch = 2,54m).
Phương pháp giải:
Gọi chiều ngang của chiếc ti vi mới là x.
Đổi các đơn vị inch sang cm
Tính chiều ngang của chiếc ti vi mới xem có vừa khoảng trống hình vuông 1m không?
Lời giải chi tiết:
- Gọi chiều ngang của chiếc ti vi mới là x
- Có 55 inch =139,7 cm
- Chiếc ti vi cũ có: chiều ngang màn hình là 72 cm
đường chéo của ti vi là: 32.2,54=81,28 (cm)
Có \(\frac{{81,28}}{{139,7}} = \frac{{72}}{x}\) => x=123,75cm=1,2375m
Vậy không thể đặt vừa chiếc ti vi vào khoảng trống hình vuông cạnh 1m
Video hướng dẫn giải
Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD=6m, AB=4m, HA=2m, AC=1m. Chứng tỏ \(\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\).
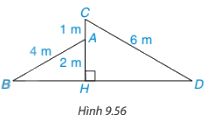
Phương pháp giải:
Chứng minhhai tam giác vuông HBA và tam giác HDC đòng dạng.
Lời giải chi tiết:
Xét hai tam giác vuông HBA và tam giác HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)
Video hướng dẫn giải
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.
Phương pháp giải:
Quan sát và sử dụng tỉ lệ của các cặp cạnh tương ứng để xác định.
Lời giải chi tiết:
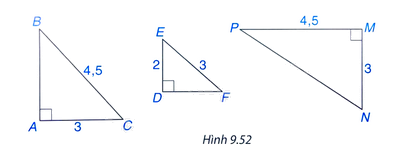
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Video hướng dẫn giải
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là AB=13m, A′B′=6,5m và độ cao lần lượt là BH=5m, B′H′=2,5m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'
- Nhận xét về hai đại lượng \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}}\)
- Dùng định lí Pythagore để tính AH và A'H'
- So sánh các đại lượng \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}}\)
- Hai tam giác vuông A'H'B' và AHB có đồng dạng không
Phương pháp giải:
- Tính các tỉ số theo yêu cầu của bài toán dựa vào độ dài đã biết.
Lời giải chi tiết:
- Có \(\frac{{A'H'}}{{AB}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
- Áp dụng định lý Pythagore có \(AH = 12 ;A'H' = 6 \)
- Có \(\frac{{A'H'}}{{AH}} = \frac{{B'H'}}{{BH}} = \frac{1}{2}\)
=> Hai tam giác vuông A'H'B' và AHB đồng dạng
Video hướng dẫn giải
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.
Phương pháp giải:
Quan sát và sử dụng tỉ lệ của các cặp cạnh tương ứng để xác định.
Lời giải chi tiết:
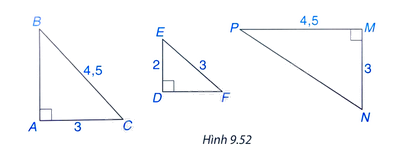
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Video hướng dẫn giải
Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD=6m, AB=4m, HA=2m, AC=1m. Chứng tỏ \(\widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\).
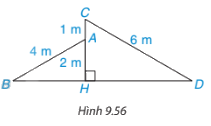
Phương pháp giải:
Chứng minhhai tam giác vuông HBA và tam giác HDC đòng dạng.
Lời giải chi tiết:
Xét hai tam giác vuông HBA và tam giác HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)
Video hướng dẫn giải
Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72cm (loại 32 inch) bằng chiếc ti vi mới loại 55 inch có cùng tỉ lệ khung hình (tỉ lệ giữa hai kích thước màn hình). Hỏi nếu khoảng trống đặt ti vi là một hình vuông cạnh 1m thì có thể đặt chiếc tivi mới vào đó không? (Biết rằng 1 inch = 2,54m).
Phương pháp giải:
Gọi chiều ngang của chiếc ti vi mới là x.
Đổi các đơn vị inch sang cm
Tính chiều ngang của chiếc ti vi mới xem có vừa khoảng trống hình vuông 1m không?
Lời giải chi tiết:
- Gọi chiều ngang của chiếc ti vi mới là x
- Có 55 inch =139,7 cm
- Chiếc ti vi cũ có: chiều ngang màn hình là 72 cm
đường chéo của ti vi là: 32.2,54=81,28 (cm)
Có \(\frac{{81,28}}{{139,7}} = \frac{{72}}{x}\) => x=123,75cm=1,2375m
Vậy không thể đặt vừa chiếc ti vi vào khoảng trống hình vuông cạnh 1m
Mục 2 của chương trình Toán 8 tập 2 - Kết nối tri thức thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các định nghĩa, tính chất và dấu hiệu nhận biết của các tứ giác này là vô cùng quan trọng để giải quyết các bài tập liên quan.
Các bài tập trên trang 100 thường yêu cầu học sinh vận dụng các tính chất của hình bình hành để tính độ dài các cạnh, số đo các góc, hoặc chứng minh một tứ giác là hình bình hành. Ví dụ, một bài tập có thể yêu cầu chứng minh rằng một tứ giác có hai cặp cạnh đối song song là hình bình hành. Để giải quyết bài tập này, học sinh cần nhớ lại định nghĩa của hình bình hành và sử dụng các tính chất về cạnh và góc của nó.
Trang 101 giới thiệu về hình chữ nhật, một loại hình bình hành đặc biệt có bốn góc vuông. Các bài tập trên trang này thường tập trung vào việc nhận biết hình chữ nhật, tính toán các yếu tố của hình chữ nhật (độ dài đường chéo, diện tích, chu vi), và chứng minh một tứ giác là hình chữ nhật. Học sinh cần nắm vững các tính chất đặc trưng của hình chữ nhật, chẳng hạn như hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Trang 102 tiếp tục giới thiệu về hình thoi, một loại hình bình hành đặc biệt có bốn cạnh bằng nhau. Các bài tập trên trang này tương tự như các bài tập về hình chữ nhật, nhưng tập trung vào các tính chất đặc trưng của hình thoi, chẳng hạn như hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. Ngoài ra, học sinh cũng cần biết cách tính diện tích của hình thoi bằng công thức: Diện tích = (1/2) * d1 * d2, trong đó d1 và d2 là độ dài của hai đường chéo.
Bài tập: Cho hình bình hành ABCD, biết AB = 5cm, BC = 3cm, góc ABC = 60 độ. Tính diện tích hình bình hành ABCD.
Giải:
Để học tốt môn Toán 8, bạn cần thường xuyên luyện tập, làm bài tập đầy đủ và tìm hiểu các phương pháp giải bài tập hiệu quả. Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu bạn gặp khó khăn. Chúc bạn học tốt!