Bài 10 trang 136 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Kết nối tri thức, yêu cầu học sinh vận dụng kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Bài tập này giúp củng cố lý thuyết và rèn luyện kỹ năng giải toán hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 136 SGK Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hình sau mô tả một dụng cụ đo bề dày (nhỏ hơn 1cm)
Đề bài
Hình sau mô tả một dụng cụ đo bề dày (nhỏ hơn 1cm) của số sản phẩm. Dụng cụ này gồm một thướng AC = 10 cm, có vạch chia đến 1 mm, gắn với một bản kim loại có cạnh thẳng AB sao cho khoảng cách BC = 1cm.
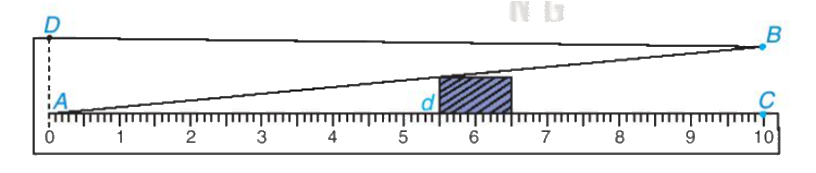
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khhi đó trên thước ta đọc đường "bề dày" d của vật (trên hình vẽ ta có d = 5,5mm). Hãy giả thích tại sao với dụng cụ đó, ta có thể đo được bề dày d của các vật (với d < 10 mm)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất hai tam giác đồng dạng
Lời giải chi tiết
Kẹp vật vào giữa bản kim loại và thước như cách sử dụng đã mô tả; ta gọi B’C’ là đoạn ứng với bề dầy d cần đo của vât (nghĩa là d = B’C’). Dễ thấy B’C’ // BC vì cùng vuông góc với AC. Do đó $\Delta AB'C'\backsim \Delta ABC$, suy ra $\frac{B'C'}{BC}=\frac{A'C'}{AC}$.
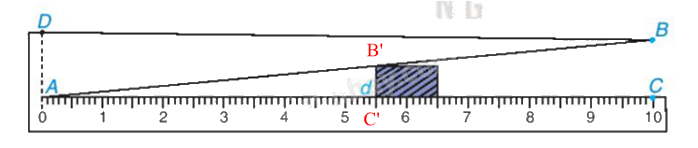
Do BC = 1 cm, AC = 10 cm nên đẳng thức này có nghĩa là B’C’ = $\frac{AC'}{10}$.
Vậy bề dày d của vật đúng bằng $\frac{1}{10}$ độ dài (cm) của AC’.
Chẳng hạn trên thức đo, AC’ = 5,5 cm có nghĩa là d = $\frac{5,5cm}{10}=5,5mm$.
Bài 10 trang 136 SGK Toán 8 tập 2 thuộc chương trình Toán 8 Kết nối tri thức, tập trung vào việc vận dụng các kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán liên quan đến tính diện tích bề mặt và thể tích. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các công thức và phương pháp sau:
Diện tích bề mặt của hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c được tính theo công thức:
Stp = 2(ab + bc + ca)
Thể tích của hình hộp chữ nhật có chiều dài a, chiều rộng b và chiều cao c được tính theo công thức:
V = abc
Diện tích bề mặt của hình lập phương có cạnh a được tính theo công thức:
Stp = 6a2
Thể tích của hình lập phương có cạnh a được tính theo công thức:
V = a3
Để giải bài 10 trang 136 SGK Toán 8 tập 2, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, áp dụng các công thức và phương pháp đã học để tìm ra lời giải chính xác.
Ví dụ: (Giả sử đề bài yêu cầu tính thể tích của một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm)
Áp dụng công thức tính thể tích hình hộp chữ nhật, ta có:
V = 5cm * 3cm * 4cm = 60cm3
Vậy thể tích của hình hộp chữ nhật là 60cm3.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em học sinh có thể tự giải thêm các bài tập sau:
Bài 10 trang 136 SGK Toán 8 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình hộp chữ nhật và hình lập phương. Bằng cách nắm vững các công thức và phương pháp giải, các em học sinh có thể tự tin giải quyết các bài toán liên quan đến chủ đề này.