Chào mừng bạn đến với bài học về lý thuyết xác suất trong chương trình Toán 8 Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về cách tính xác suất của một biến cố bằng tỉ số, giúp bạn giải quyết các bài toán thực tế một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, công thức và các ví dụ minh họa để nắm vững kiến thức này.
Tính xác suất bằng tỉ số như thế nào?
Tính xác suất bằng tỉ số
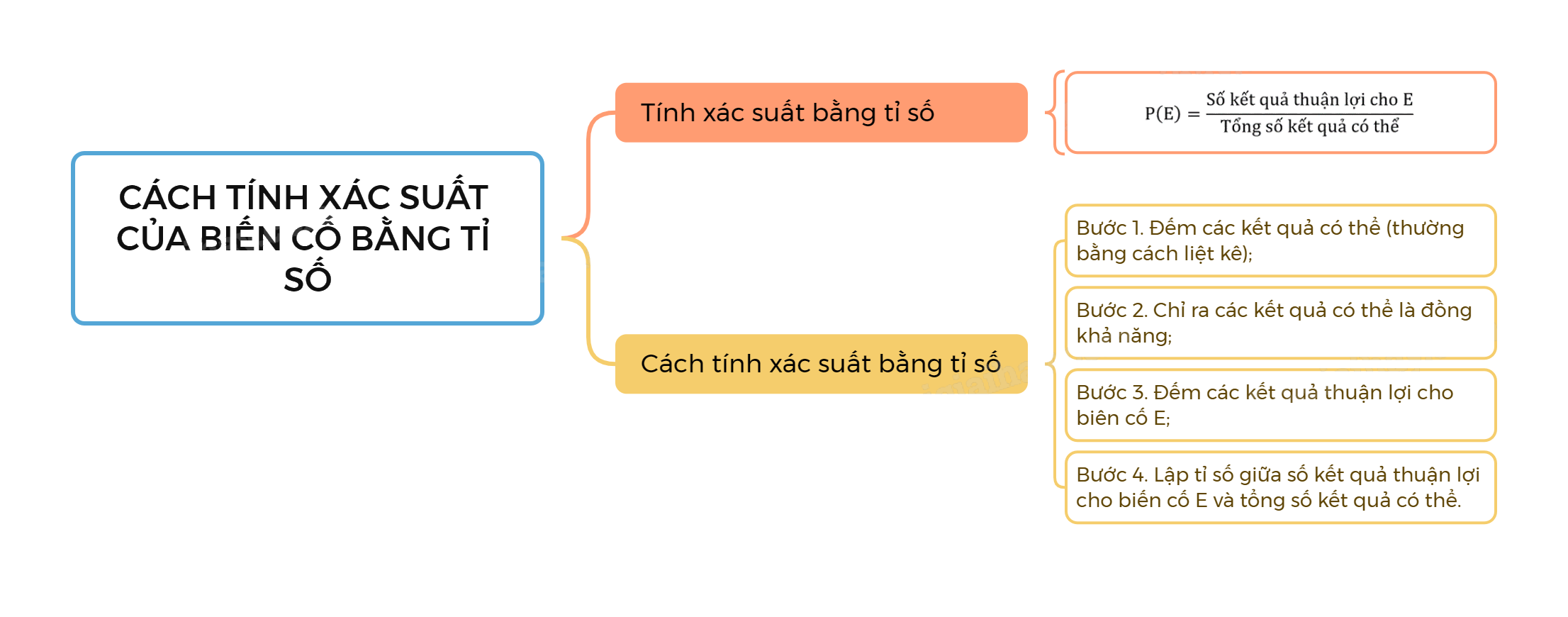
Giả thiết rằng các kết quả có thể của một hành động hay thực nghiệm là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu là P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
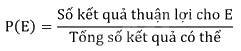
Cách tính xác suất bằng tỉ số
Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm đồng khả năng sẽ gồm các bước sau:
Bước 1. Đếm các kết quả có thể (thường bằng cách liệt kê);
Bước 2. Chỉ ra các kết quả có thể là đồng khả năng;
Bước 3. Đếm các kết quả thuận lợi cho biên cố E;
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
Ví dụ: Gieo một con xúc xắc.
Các kết quả có thể của hành động trên là 1, 2, 3, 4, 5, 6 chấm. Có 6 kết quả có thể.
Biến cố E: “Gieo được số chấm lẻ” xảy ra khi gieo được các số lẻ. Do đó các kết quả thuận lợi cho biến cố E là 1, 3, 5. Có 3 kết quả thuận lợi
Xác suất của biến cố E là: \(P(E) = \frac{3}{6} = \frac{1}{2}\)
Xác suất là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong đời sống. Trong chương trình Toán 8 Kết nối tri thức, học sinh được giới thiệu về cách tính xác suất của một biến cố bằng tỉ số. Bài viết này sẽ trình bày chi tiết về lý thuyết này, bao gồm định nghĩa, công thức và các ví dụ minh họa.
Trước khi đi vào cách tính xác suất, chúng ta cần hiểu rõ hai khái niệm cơ bản là biến cố và không gian mẫu.
Xác suất của một biến cố A, ký hiệu là P(A), là tỉ số giữa số các kết quả có lợi cho A và số các kết quả có thể xảy ra trong không gian mẫu. Công thức tính xác suất được biểu diễn như sau:
P(A) = (Số các kết quả có lợi cho A) / (Số các kết quả có thể xảy ra)
Ví dụ 1: Tung một con xúc xắc 6 mặt. Tính xác suất để tung được mặt 5 chấm.
Giải:
Ví dụ 2: Rút một lá bài từ bộ bài 52 lá. Tính xác suất để rút được lá át.
Giải:
Bài 1: Một hộp có 8 quả bóng, trong đó có 5 quả bóng màu đỏ và 3 quả bóng màu xanh. Lấy ngẫu nhiên một quả bóng từ hộp. Tính xác suất để lấy được quả bóng màu đỏ.
Bài 2: Gieo một đồng xu hai lần liên tiếp. Tính xác suất để cả hai lần đều được mặt ngửa.
Lý thuyết về cách tính xác suất của biến cố bằng tỉ số là một kiến thức cơ bản và quan trọng trong toán học. Việc nắm vững lý thuyết này sẽ giúp học sinh giải quyết các bài toán liên quan đến xác suất một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.