Bài 9.27 trang 103 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng thực tế của phương trình bậc nhất một ẩn. Bài tập này thường yêu cầu học sinh xây dựng phương trình để mô tả một tình huống thực tế và giải phương trình đó để tìm ra giá trị cần tìm.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.27 Toán 8 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác A'B'C' đồng dạng với tam giác ABC
Đề bài
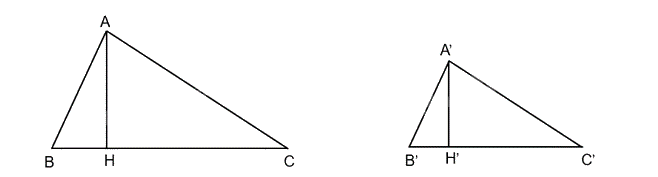
Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:
a) \(\frac{{A'H'}}{{AH}} = k\)
b) Diện tích tam giác A'B'C' bằng \(k^2\) lần diện tích tam giác ABC
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B'};\frac{{A'H'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Chứng minh ΔA′H′B′ ∽ ΔAHB suy ra các hệ số tỉ lệ và chứng minh được \(\frac{{A'H'}}{{AH}} = k\)
b) Tính diện tích tam giác ABC và A”B”C” từ đó sẽ xét tỉ số diện tích của hai tam giác đó.
Lời giải chi tiết
a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B'};\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có:
\(\widehat B = \widehat {B'}\)
=> ΔA′H′B′ ∽ ΔAHB
=> \(\frac{{A'H'}}{{AH}} = \frac{{A'B'}}{{AB}}\)
Mà \(\frac{{A'B'}}{{AB}} = k\)
=> \(\frac{{A'H'}}{{AH}} = k\)
b) Có diện tích tam giác ABC là: \(\frac{1}{2}\)AH.BC
Có diện tích tam giác A'B'C' là: \(\frac{1}{2}\)A′H′.B′C′
Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có:
\(\frac{{\frac{1}{2}A'H'.B'C'}}{{\frac{1}{2}AH.BC}} = \frac{{A'H'}}{{AH}}.\frac{{B'C'}}{{BC}} = k.k = {k^2}\)
Bài 9.27 trang 103 SGK Toán 8 tập 2 - Kết nối tri thức là một bài toán thực tế, yêu cầu học sinh vận dụng kiến thức về phương trình bậc nhất một ẩn để giải quyết. Dưới đây là hướng dẫn chi tiết từng bước để giải bài toán này:
Đề bài thường mô tả một tình huống cụ thể liên quan đến một đại lượng chưa biết. Nhiệm vụ của học sinh là xác định đại lượng đó và xây dựng phương trình để biểu diễn mối quan hệ giữa các đại lượng trong tình huống.
Bước quan trọng đầu tiên là xác định ẩn số, tức là đại lượng mà chúng ta cần tìm. Ký hiệu ẩn số bằng một chữ cái, ví dụ x.
Dựa vào mối quan hệ giữa các đại lượng trong đề bài, ta lập phương trình để biểu diễn mối quan hệ đó. Phương trình phải chứa ẩn số đã xác định.
Sử dụng các quy tắc giải phương trình bậc nhất một ẩn để tìm ra giá trị của ẩn số. Các bước giải phương trình bao gồm:
Sau khi tìm được giá trị của ẩn số, ta cần kiểm tra lại kết quả bằng cách thay giá trị đó vào phương trình ban đầu để xem phương trình có đúng không. Nếu phương trình đúng, kết quả là chính xác.
Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau 1 giờ 30 phút, người đó còn cách B 20km. Tính quãng đường AB.
Giải:
Vậy, quãng đường AB là 80km.
Ngoài bài 9.27, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về phương trình bậc nhất một ẩn để giải quyết các tình huống thực tế. Các bài tập này có thể liên quan đến các lĩnh vực khác nhau như:
Để giải bài tập về phương trình bậc nhất một ẩn hiệu quả, học sinh cần:
Ngoài SGK Toán 8 tập 2 - Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 9.27 trang 103 SGK Toán 8 tập 2 - Kết nối tri thức và các bài tập tương tự. Chúc các em học tập tốt!