Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 53, 54 sách giáo khoa Toán 8 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em tự tin hơn trong quá trình học tập và làm bài tập về nhà.
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai
Tìm các cặp đường thẳng song song với nhau trong các đường thẳng sau:
a) y = 2x + 1;
b) y = -1 - 2x;
c) y = 2 + 2x;
d) y = -1 + 2x.
Phương pháp giải:
Hai đường thẳng y = ax + b (a \(\ne\) 0) và y = a'x + b' (a' \(\ne\) 0) song song với nhau khi a = a', b \(\ne\) b' và ngược lại.
Lời giải chi tiết:
Hai đường thẳng
a) y = 2x + 1 và c) y = 2 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (1 \(\ne\) 2)
a) y = 2x + 1 và d) y = -1 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (1 \(\ne\) -1)
c) y = 2 + 2x và d) y = -1 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (2 \(\ne\) -1)
Video hướng dẫn giải
Cho hai đường thẳng y=2x-1 và y=x-3. Bằng cách so sánh hai hệ số góc, hãy cho biết hai đường thẳng này có song song hay trùng nhau không
Phương pháp giải:
Xác định hệ số góc của hai đường thẳng đã cho và so sánh.
Lời giải chi tiết:
Đường thẳng y=2x-1 có hệ số góc a = 2 và đường thẳng y=x – 3 có hệ số góc a’=1
Vì a≠a′ => Ha đường thẳng này không song song và không trùng nhau
Liệu hai đường thẳng phân biệt có cùng hệ số góc, có thể có
a) Cùng giao điểm với trục Ox không?
b) Cùng giao điểm với trục Oy không?
Phương pháp giải:
Hai đường thẳng phân biệt có cùng hệ số góc nên hai đường thẳng đó song song với nhau
Lời giải chi tiết:
Hai đường thẳng phân biệt có cùng hệ số góc nên hai đường thẳng đó song song với nhau. Vậy hai đường thẳng đó không có cùng giao điểm với trục Ox, Oy được
Video hướng dẫn giải
Cho hai hàm số bậc nhất y=2mx+1 và y=(m−1)x+2. Tìm các giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau
b) Hai đường thẳng cắt nhau
Phương pháp giải:
Hai đường thẳng \(y = {\rm{ax + b(a}} \ne {\rm{0)}}\)và \(y = a'x + b'\left( {a' \ne 0} \right)\)song song với nhau khi a = a’; cắt nhau khi \(a \ne a'\)
Lời giải chi tiết:
Hai đường thẳng song song khi a=a′ => 2m=m−1
=> m=−1
b) Hai đường thẳng cắt nhau khi a≠a′ =>2m≠m−1
=> m≠−1
Video hướng dẫn giải
Vuông: Làm thế nào để biết hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) song song hay cắt nhau nhỉ?
Tròn: Cứ vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ Oxy là biết ngay mà.
Pi: Anh có một cách nhanh hơn nhiều mà không cần vẽ hình. Trong bài học này chúng ta sẽ cùng tìm hiểu nhé.
Em hãy trình bày cách làm của Pi để trả lời câu hỏi của bạn Vuông
Phương pháp giải:
Dựa vào hệ số góc để xem khi nào hai đường thẳng cắt nhau; hai đường thẳng song song
Lời giải chi tiết:
Hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) có a = a’ ; \(b \ne b'\) thì hai đường thẳng đó song song với nhau.
Hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) có \(a \ne a'\) thì hai đường thẳng đó cắt nhau.
Video hướng dẫn giải
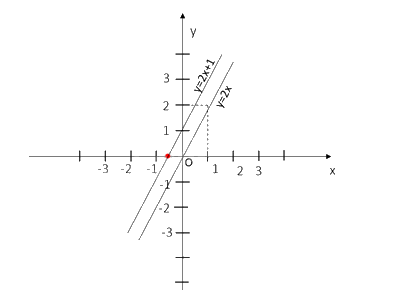
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng y=2x và y=2x+1. Có nhận xét gì về vị trí tương đối của hai đường thẳng này
Phương pháp giải:
Xác định hai điểm thuộc đường thẳng y = 2x và hai điểm thuộc đường thẳng y = -2x + 1.
Quan sát vị trí tương đối của hai đường thẳng đó
Lời giải chi tiết:
* Xét đường thẳng y = 2x
Cho x = 0 suy ra y = 2.0 = 0 nên điểm (0; 0) thuộc đường thẳng y = 2x
Cho x = 1 suy ra y = 2 nên điểm (1; 2) thuộc đường thẳng y = 2x
Đường thẳng y=2x đi qua 2 điểm (0;0) và (1;2)
* Xét đường thẳng y = 2x + 1
Cho x = 0 suy ra y = 2.0 + 1= 1 nên điểm (0; 1) thuộc đường thẳng y = 2x + 1
Cho \(x = \frac{{ - 1}}{2}\) suy ra \(y = 2.\left( {\frac{{ - 1}}{2}} \right) + 1 = 0\) nên điểm \(\left( {\frac{{ - 1}}{2};0} \right)\) thuộc đường thẳng y = 2x + 1
Đường thẳng y=2x+1 đi qua 2 điểm (−12;0) và (0;1)
Tìm các cặp đường thẳng song song với nhau trong các đường thẳng sau:
a) y = 2x + 1;
b) y = -1 - 2x;
c) y = 2 + 2x;
d) y = -1 + 2x.
Phương pháp giải:
Hai đường thẳng y = ax + b (a \(\ne\) 0) và y = a'x + b' (a' \(\ne\) 0) song song với nhau khi a = a', b \(\ne\) b' và ngược lại.
Lời giải chi tiết:
Hai đường thẳng
a) y = 2x + 1 và c) y = 2 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (1 \(\ne\) 2)
a) y = 2x + 1 và d) y = -1 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (1 \(\ne\) -1)
c) y = 2 + 2x và d) y = -1 + 2x song song với nhau vì có a = a' = 2, b \(\ne\) \b' (2 \(\ne\) -1)
Video hướng dẫn giải
Cho hai đường thẳng y=2x-1 và y=x-3. Bằng cách so sánh hai hệ số góc, hãy cho biết hai đường thẳng này có song song hay trùng nhau không
Phương pháp giải:
Xác định hệ số góc của hai đường thẳng đã cho và so sánh.
Lời giải chi tiết:
Đường thẳng y=2x-1 có hệ số góc a = 2 và đường thẳng y=x – 3 có hệ số góc a’=1
Vì a≠a′ => Ha đường thẳng này không song song và không trùng nhau
Video hướng dẫn giải
Cho hai hàm số bậc nhất y=2mx+1 và y=(m−1)x+2. Tìm các giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau
b) Hai đường thẳng cắt nhau
Phương pháp giải:
Hai đường thẳng \(y = {\rm{ax + b(a}} \ne {\rm{0)}}\)và \(y = a'x + b'\left( {a' \ne 0} \right)\)song song với nhau khi a = a’; cắt nhau khi \(a \ne a'\)
Lời giải chi tiết:
Hai đường thẳng song song khi a=a′ => 2m=m−1
=> m=−1
b) Hai đường thẳng cắt nhau khi a≠a′ =>2m≠m−1
=> m≠−1
Liệu hai đường thẳng phân biệt có cùng hệ số góc, có thể có
a) Cùng giao điểm với trục Ox không?
b) Cùng giao điểm với trục Oy không?
Phương pháp giải:
Hai đường thẳng phân biệt có cùng hệ số góc nên hai đường thẳng đó song song với nhau
Lời giải chi tiết:
Hai đường thẳng phân biệt có cùng hệ số góc nên hai đường thẳng đó song song với nhau. Vậy hai đường thẳng đó không có cùng giao điểm với trục Ox, Oy được
Video hướng dẫn giải
Vuông: Làm thế nào để biết hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) song song hay cắt nhau nhỉ?
Tròn: Cứ vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ Oxy là biết ngay mà.
Pi: Anh có một cách nhanh hơn nhiều mà không cần vẽ hình. Trong bài học này chúng ta sẽ cùng tìm hiểu nhé.
Em hãy trình bày cách làm của Pi để trả lời câu hỏi của bạn Vuông
Phương pháp giải:
Dựa vào hệ số góc để xem khi nào hai đường thẳng cắt nhau; hai đường thẳng song song
Lời giải chi tiết:
Hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) có a = a’ ; \(b \ne b'\) thì hai đường thẳng đó song song với nhau.
Hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) có \(a \ne a'\) thì hai đường thẳng đó cắt nhau.
Video hướng dẫn giải
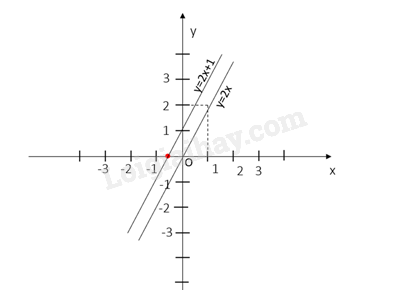
Trên cùng một mặt phẳng tọa độ Oxy, vẽ hai đường thẳng y=2x và y=2x+1. Có nhận xét gì về vị trí tương đối của hai đường thẳng này
Phương pháp giải:
Xác định hai điểm thuộc đường thẳng y = 2x và hai điểm thuộc đường thẳng y = -2x + 1.
Quan sát vị trí tương đối của hai đường thẳng đó
Lời giải chi tiết:
* Xét đường thẳng y = 2x
Cho x = 0 suy ra y = 2.0 = 0 nên điểm (0; 0) thuộc đường thẳng y = 2x
Cho x = 1 suy ra y = 2 nên điểm (1; 2) thuộc đường thẳng y = 2x
Đường thẳng y=2x đi qua 2 điểm (0;0) và (1;2)
* Xét đường thẳng y = 2x + 1
Cho x = 0 suy ra y = 2.0 + 1= 1 nên điểm (0; 1) thuộc đường thẳng y = 2x + 1
Cho \(x = \frac{{ - 1}}{2}\) suy ra \(y = 2.\left( {\frac{{ - 1}}{2}} \right) + 1 = 0\) nên điểm \(\left( {\frac{{ - 1}}{2};0} \right)\) thuộc đường thẳng y = 2x + 1
Đường thẳng y=2x+1 đi qua 2 điểm (−12;0) và (0;1)
Mục 2 trang 53, 54 SGK Toán 8 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Tam giác đồng dạng. Nội dung chính bao gồm việc nhắc lại các định nghĩa, tính chất của tam giác đồng dạng, các trường hợp đồng dạng của tam giác và ứng dụng của tam giác đồng dạng trong việc giải toán.
Mục 2 bao gồm các bài tập rèn luyện kỹ năng nhận biết, vận dụng các kiến thức về tam giác đồng dạng để giải quyết các bài toán thực tế. Các bài tập thường yêu cầu học sinh:
Bài 1 yêu cầu học sinh nhắc lại các định nghĩa, tính chất của tam giác đồng dạng. Đây là bài tập cơ bản giúp học sinh củng cố kiến thức nền tảng.
Bài 2 tập trung vào việc vận dụng các trường hợp đồng dạng của tam giác (g-g, g-g-g, c-c) để chứng minh hai tam giác đồng dạng. Học sinh cần phân tích kỹ đề bài để lựa chọn trường hợp đồng dạng phù hợp.
Bài 3 yêu cầu học sinh tính độ dài các đoạn thẳng khi biết tỉ lệ đồng dạng của hai tam giác. Đây là bài tập ứng dụng thực tế của tam giác đồng dạng.
Bài 4 là bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức về tam giác đồng dạng để giải quyết các bài toán hình học phức tạp hơn. Học sinh cần kết hợp các kiến thức đã học để tìm ra lời giải.
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 2:
Tam giác ABC đồng dạng với tam giác A'B'C' (ký hiệu: ΔABC ~ ΔA'B'C') nếu:
Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Gọi D là điểm trên BC sao cho BD = 1cm. Chứng minh tam giác ABD đồng dạng với tam giác ABC.
Giải:
Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số 2/3. Biết AB = 4cm, BC = 6cm, CA = 8cm. Tính độ dài các cạnh của tam giác A'B'C'.
Giải:
A'B' = (2/3) * AB = (2/3) * 4 = 8/3 cm
B'C' = (2/3) * BC = (2/3) * 6 = 4 cm
C'A' = (2/3) * CA = (2/3) * 8 = 16/3 cm
Việc nắm vững kiến thức về tam giác đồng dạng là rất quan trọng trong chương trình Toán 8. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về tam giác đồng dạng, đặc biệt là các bài tập trong mục 2 trang 53, 54 SGK Toán 8 tập 2 - Kết nối tri thức.