Bài 10.14 trang 122 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng tính chất của hình thang cân. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về các yếu tố của hình thang cân và cách vận dụng chúng vào giải quyết bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre
Đề bài
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m
a) Tính thể tích hình chóp
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31, 92m.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Vẽ hình kim tự tháp để minh họa.
- Áp dụng công thức tính thể tích hình chóp.
- Tổng diện tích các tâm kính để phủ kín bốn mặt bên hình chóp là diẹn tích xung quanh của hình chóp.
Lời giải chi tiết
- Có hình vẽ minh họa cho kim tự tháp
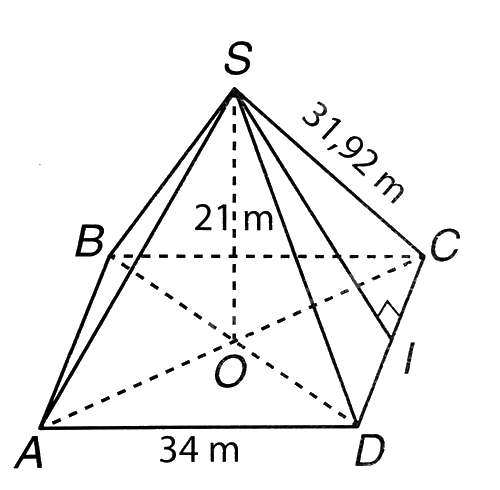
a) Thể tích hình chóp tứ giác đều là:
$V=\frac{1}{3}{{S}_{đáy}}.h=\frac{1}{3}{{.34}^{2}}.21=8092\left( c{{m}^{3}} \right)$
b) CI = 17m.
Áp dụng định lí Pythagore cho tam giác SCI vuông tại I, ta có:
CI2 + SI2 = SC2
172 + SI2 = 31,922
SI2 = 729,89
SI = 27,02
Diện tích xung quanh của hình chóp tứ giác đều là:
\[{{S}_{xq}}=pd\approx \frac{34.4}{2}.27,02=1837,36\left( {{m}^{2}} \right)\].
Bài 10.14 SGK Toán 8 tập 2 Kết nối tri thức yêu cầu chúng ta chứng minh một tính chất quan trọng của hình thang cân. Cụ thể, bài toán cho hình thang cân ABCD (AB // CD) và đường thẳng d vuông góc với AB tại E, đường thẳng d vuông góc với CD tại F. Yêu cầu là chứng minh rằng EF là đường trung bình của hình thang cân ABCD.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để chứng minh EF là đường trung bình của hình thang cân ABCD, chúng ta cần chứng minh E và F lần lượt là trung điểm của AD và BC. Vì d vuông góc với AB và CD, ta có AE = DE và BF = CF. Do đó, nếu chứng minh được AE = BF, ta có thể kết luận E và F là trung điểm của AD và BC.
Chứng minh:
Để hiểu sâu hơn về bài toán này, các em có thể thử giải các bài tập tương tự sau:
Bài 10.14 trang 122 SGK Toán 8 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân và đường trung bình của hình thang. Việc nắm vững lý thuyết và phương pháp giải bài tập này sẽ giúp các em tự tin hơn trong quá trình học tập môn Toán.