Chào mừng bạn đến với bài học về Lý thuyết Hình chữ nhật trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đầy đủ và chi tiết các kiến thức cơ bản về hình chữ nhật, bao gồm định nghĩa, tính chất, dấu hiệu nhận biết và các ứng dụng thực tế.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập hiệu quả và thú vị với phương pháp trình bày dễ hiểu, bài tập đa dạng và đáp án chính xác.
Hình chữ nhật là gì?
1. Khái niệm

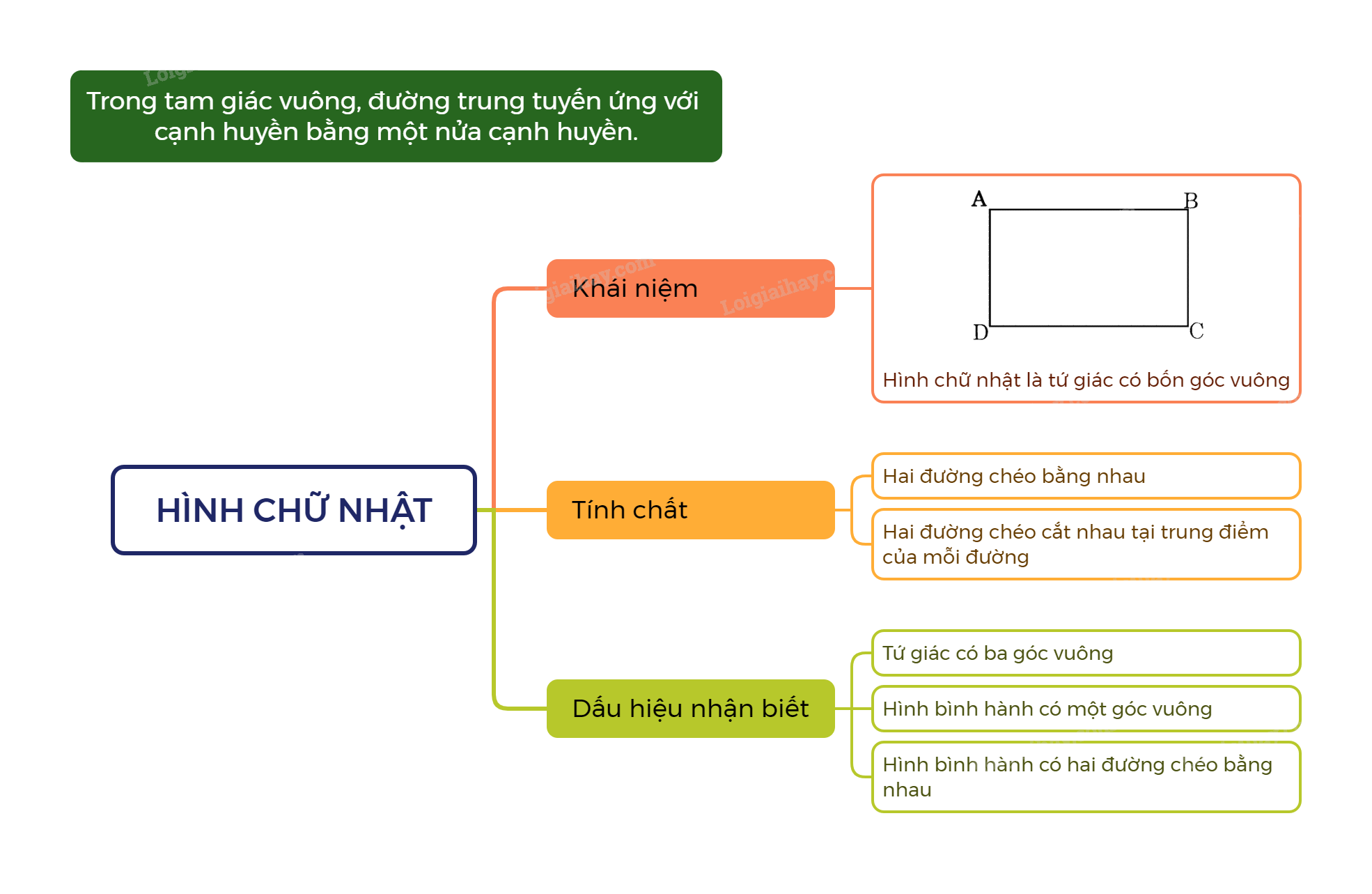
Hình chữ nhật là tứ giác có bốn góc vuông.
Chú ý:Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông và tứ giác đó là hình chữ nhật.
2. Tính chất
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Nhận xét:Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
3. Dấu hiệu nhận biết
- Hình bình hành có một góc vuông là hình chữ nhật
- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
Ví dụ:

Hình b là hình chữ nhật vì có 4 góc vuông.
Hình chữ nhật là một trong những hình học cơ bản và quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết về hình chữ nhật không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho việc học các kiến thức hình học nâng cao hơn.
Hình chữ nhật là tứ giác có bốn góc vuông. Điều này có nghĩa là mỗi góc của hình chữ nhật đều bằng 90 độ.
Hình chữ nhật là một trường hợp đặc biệt của hình bình hành. Mọi hình chữ nhật đều là hình bình hành, nhưng không phải mọi hình bình hành đều là hình chữ nhật. Hình chữ nhật là hình bình hành có một góc vuông.
Hình chữ nhật xuất hiện rất nhiều trong cuộc sống hàng ngày. Ví dụ:
Để củng cố kiến thức về hình chữ nhật, bạn có thể thực hiện các bài tập sau:
Ngoài lý thuyết cơ bản, bạn có thể tìm hiểu thêm về các khái niệm liên quan đến hình chữ nhật như:
Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về Lý thuyết Hình chữ nhật SGK Toán 8 - Kết nối tri thức. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế. Chúc bạn học tập tốt!