Bài 4.4 trang 80 SGK Toán 8 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các định lý về hình bình hành và các tính chất liên quan. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán thực tế liên quan đến hình bình hành.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.4 trang 80 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho ∆ABC có trọng tâm G.
Đề bài
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng \(BM = \dfrac{1}{3}BC\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất trọng tâm G trong tam giác ABC và định lí Thalès vì MG //AB
Lời giải chi tiết
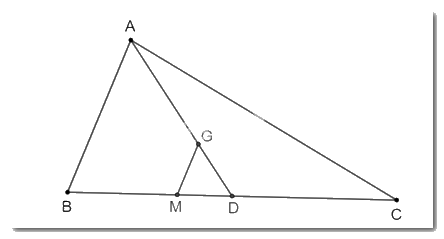
Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{2}{3}\) hay \(AG = \dfrac{2}{3}A{\rm{D}}\)
Vì MG // AB, theo định lí Thalès, ta suy ra: \(\dfrac{{AG}}{{A{\rm{D}}}} = \dfrac{{BM}}{{B{\rm{D}}}} = \dfrac{2}{3}\)
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên \(\dfrac{{BM}}{{BC}} = \dfrac{{BM}}{{2B{\rm{D}}}} = \dfrac{2}{{2.3}} = \dfrac{1}{3}\)
Do đó \(BM = \dfrac{1}{3}BC\) (đpcm).
Bài 4.4 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hình bình hành, đặc biệt là các định lý liên quan đến tính chất đường chéo, góc và cạnh của hình bình hành. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào các bài toán cụ thể.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định hình bình hành nào được đề cập, các yếu tố nào đã cho và cần tìm gì. Việc phân tích đề bài giúp học sinh có cái nhìn tổng quan và lựa chọn phương pháp giải phù hợp.
(Nội dung lời giải chi tiết bài 4.4 sẽ được trình bày tại đây, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ:)
Bài 4.4: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng:
Lời giải:
a) Xét tam giác ABC, E là trung điểm của AB và F là giao điểm của DE và AC. Áp dụng định lý Menelaus cho tam giác ABC với đường thẳng DE, ta có:
(AE/EB) * (BD/DC) * (CF/FA) = 1
Vì E là trung điểm của AB nên AE/EB = 1. Vì ABCD là hình bình hành nên BD/DC = 1. Do đó:
1 * 1 * (CF/FA) = 1 => CF/FA = 1 => CF = FA. Vậy F là trung điểm của AC.
b) Vì F là trung điểm của AC nên AF = FC.
Ngoài bài 4.4, học sinh có thể gặp các bài tập tương tự liên quan đến hình bình hành, yêu cầu chứng minh các tính chất hoặc giải các bài toán thực tế. Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hình bình hành, học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc luyện tập thường xuyên giúp học sinh nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong SGK Toán 8 tập 1 - Kết nối tri thức và các chương trình học khác. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong học tập.
Hãy truy cập Giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và lời giải bài tập Toán 8!