Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 59, 60, 61 sách giáo khoa Toán 8 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
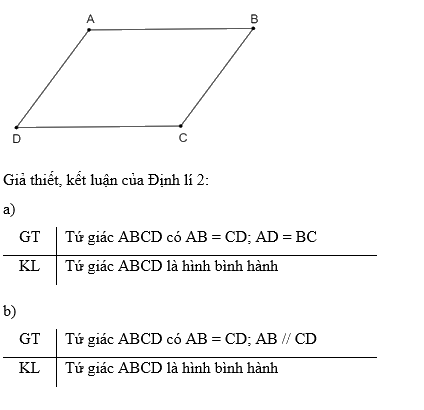
Hãy viết giả thiết, kết luận của Định lí 2.
Video hướng dẫn giải
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
Phương pháp giải:
Chứng minh tứ giác ABA’B’ là hình bình hành
Lời giải chi tiết:
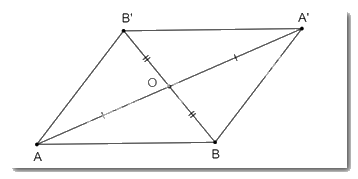
Ta hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB.
Mà O là trung điểm của AA’, BB’ nên O là trung điểm của hai đường chéo của tứ giác ABA’B’.
Do đó tứ giác ABA’B’ là hình bình hành.
Video hướng dẫn giải
Hãy biết giả thiết, kết luận của Định lí 3.
Phương pháp giải:
Dựa vào định lí 3 vẽ hình và ghi giả thiết kết luận
Lời giải chi tiết:
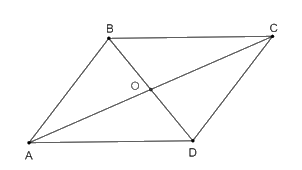
Giả thiết, kết luận của Định lí 3:
a)
GT | Tứ giác ABCD có \(\widehat A = \widehat C;\widehat B = \widehat D\) | |
KL | Tứ giác ABCD là hình bình hành | |
b)
GT | Tứ giác ABCD có AC cắt BD tại điểm O; OA = OC; OB = OD. | |
KL | Tứ giác ABCD là hình bình hành | |
Video hướng dẫn giải
Chia một sợi dây xích thành bốn đoạn: hai đoạn dài bằng nhau, hai đoạn ngắn bằng nhau và đoạn dài, đoạn ngắn xen kẽ nhau. Hỏi khi móc hai đầu mút của sợi dây xích đó lại để được một tứ giác ABCD (có các đỉnh tại các điểm chia) như Hình 3.33 thì tứ giác ABCD là hình gì? Tại sao?
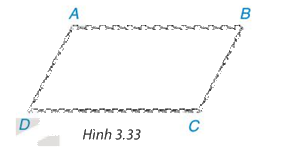
Phương pháp giải:
Chứng minh tứ giác ABCD có các cặp góc đối bằng nhau nên ABCD là hình bình hành.
Lời giải chi tiết:
Đoạn dây xích được chia thành:
• Hai đoạn dài có độ dài bằng nhau, tức là AB = CD;
• Hai đoạn ngắn có độ dài bằng nhau, tức là AD = BC.
Tứ giác ABCD có AB = CD; AD = BC nên tứ giác ABCD là hình bình hành.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của Định lí 2.
Phương pháp giải:
Dựa vào định lí 2 vẽ hình và ghi giả thiết kết luận
Lời giải chi tiết:

Video hướng dẫn giải
Trở lại bài toán mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở đi qua O sao cho theo con đường đó, hai đoạn đường từ O tới a và tới b bằng nhau.
Phương pháp giải:
- Vẽ bài toán theo yêu câu
- Chứng minh tứ giác ABCD là hình bình hành
Lời giải chi tiết:
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
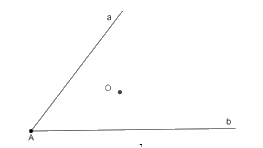
- Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
- Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D.
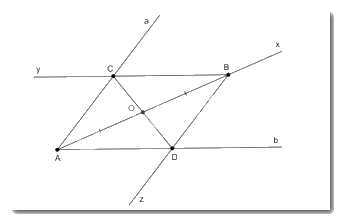
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.
Video hướng dẫn giải
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32).
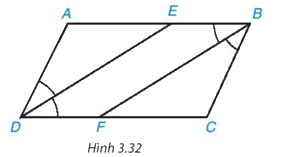
a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau.
b) Tứ giác DEBF là hình gì? Tại sao?
Phương pháp giải:
a) Sử dụng tính chất của hình bình hành để chứng minh tam giác ADE, CBF là tam giác cân.
b) Chứng minh tứ giác DEBF có các cặp cạnh đối song song với nhan nên tứ giác DEBF là hình bình hành.
Lời giải chi tiết:
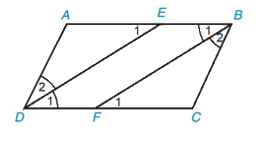
a) Vì ABCD là hình bình hành nên AB // CD hay BE // DF.
Vì DE là tia phân giác của \(\widehat {A{\rm{D}}C}\) nên \(\widehat {{D_1}} = \widehat {{D_2}}\)
Mà \(\widehat {{D_1}} = \widehat {{E_1}}\) (BE // DF, hai góc so le trong) nên \(\widehat {{D_2}} = \widehat {{E_1}}\)
Suy ra tam giác ADE cân tại A.
Tương tự ta cũng chứng minh được: tam giác BCF cân tại C.
Vì ABCD là hình bình hành nên AD = BC; \(\widehat A = \widehat C;\widehat {A{\rm{D}}C} = \widehat {ABC}\).
Vì AE là tia phân giác \(\widehat {A{\rm{D}}C}\); BF là tia phân giác \(\widehat {ABC}\) nên
\(\widehat {{B_1}} = \widehat {{B_2}};\widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {A{\rm{D}}C} = \widehat {ABC}\)
Do đó \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\)
Xét ∆ADE và ∆CBF có:
\(\widehat A = \widehat C\)(chứng minh trên);
AD = BC (chứng minh trên);
\(\widehat {{B_2}} = \widehat {{D_2}}\) (chứng minh trên).
Do đó ∆ADE = ∆CBF (g.c.g).
b) Vì \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {{B_2}} = \widehat {{F_1}}\) (vì tam giác BCF cân tại C)
Suy ra \(\widehat {{D_1}} = \widehat {{F_1}}\) (hai góc đồng vị).
Do đó DE // BF.
Tứ giác BEDF có:
BE // DF (chứng minh trên);
DE // BF (chứng minh trên).
Do đó, tứ giác BEDF là hình bình hành.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của Định lí 2.
Phương pháp giải:
Dựa vào định lí 2 vẽ hình và ghi giả thiết kết luận
Lời giải chi tiết:
Video hướng dẫn giải
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32).
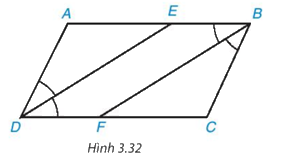
a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau.
b) Tứ giác DEBF là hình gì? Tại sao?
Phương pháp giải:
a) Sử dụng tính chất của hình bình hành để chứng minh tam giác ADE, CBF là tam giác cân.
b) Chứng minh tứ giác DEBF có các cặp cạnh đối song song với nhan nên tứ giác DEBF là hình bình hành.
Lời giải chi tiết:
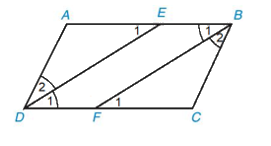
a) Vì ABCD là hình bình hành nên AB // CD hay BE // DF.
Vì DE là tia phân giác của \(\widehat {A{\rm{D}}C}\) nên \(\widehat {{D_1}} = \widehat {{D_2}}\)
Mà \(\widehat {{D_1}} = \widehat {{E_1}}\) (BE // DF, hai góc so le trong) nên \(\widehat {{D_2}} = \widehat {{E_1}}\)
Suy ra tam giác ADE cân tại A.
Tương tự ta cũng chứng minh được: tam giác BCF cân tại C.
Vì ABCD là hình bình hành nên AD = BC; \(\widehat A = \widehat C;\widehat {A{\rm{D}}C} = \widehat {ABC}\).
Vì AE là tia phân giác \(\widehat {A{\rm{D}}C}\); BF là tia phân giác \(\widehat {ABC}\) nên
\(\widehat {{B_1}} = \widehat {{B_2}};\widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {A{\rm{D}}C} = \widehat {ABC}\)
Do đó \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\)
Xét ∆ADE và ∆CBF có:
\(\widehat A = \widehat C\)(chứng minh trên);
AD = BC (chứng minh trên);
\(\widehat {{B_2}} = \widehat {{D_2}}\) (chứng minh trên).
Do đó ∆ADE = ∆CBF (g.c.g).
b) Vì \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {{B_2}} = \widehat {{F_1}}\) (vì tam giác BCF cân tại C)
Suy ra \(\widehat {{D_1}} = \widehat {{F_1}}\) (hai góc đồng vị).
Do đó DE // BF.
Tứ giác BEDF có:
BE // DF (chứng minh trên);
DE // BF (chứng minh trên).
Do đó, tứ giác BEDF là hình bình hành.
Video hướng dẫn giải
Chia một sợi dây xích thành bốn đoạn: hai đoạn dài bằng nhau, hai đoạn ngắn bằng nhau và đoạn dài, đoạn ngắn xen kẽ nhau. Hỏi khi móc hai đầu mút của sợi dây xích đó lại để được một tứ giác ABCD (có các đỉnh tại các điểm chia) như Hình 3.33 thì tứ giác ABCD là hình gì? Tại sao?
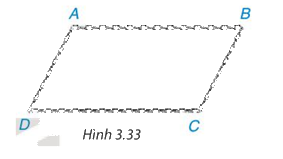
Phương pháp giải:
Chứng minh tứ giác ABCD có các cặp góc đối bằng nhau nên ABCD là hình bình hành.
Lời giải chi tiết:
Đoạn dây xích được chia thành:
• Hai đoạn dài có độ dài bằng nhau, tức là AB = CD;
• Hai đoạn ngắn có độ dài bằng nhau, tức là AD = BC.
Tứ giác ABCD có AB = CD; AD = BC nên tứ giác ABCD là hình bình hành.
Video hướng dẫn giải
Hãy biết giả thiết, kết luận của Định lí 3.
Phương pháp giải:
Dựa vào định lí 3 vẽ hình và ghi giả thiết kết luận
Lời giải chi tiết:
Giả thiết, kết luận của Định lí 3:
a)
GT | Tứ giác ABCD có \(\widehat A = \widehat C;\widehat B = \widehat D\) | |
KL | Tứ giác ABCD là hình bình hành | |
b)
GT | Tứ giác ABCD có AC cắt BD tại điểm O; OA = OC; OB = OD. | |
KL | Tứ giác ABCD là hình bình hành | |
Video hướng dẫn giải
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
Phương pháp giải:
Chứng minh tứ giác ABA’B’ là hình bình hành
Lời giải chi tiết:
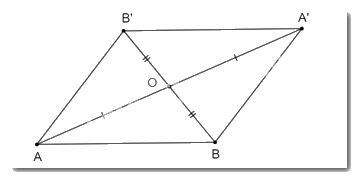
Ta hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB.
Mà O là trung điểm của AA’, BB’ nên O là trung điểm của hai đường chéo của tứ giác ABA’B’.
Do đó tứ giác ABA’B’ là hình bình hành.
Video hướng dẫn giải
Trở lại bài toán mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở đi qua O sao cho theo con đường đó, hai đoạn đường từ O tới a và tới b bằng nhau.
Phương pháp giải:
- Vẽ bài toán theo yêu câu
- Chứng minh tứ giác ABCD là hình bình hành
Lời giải chi tiết:
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
- Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
- Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D.
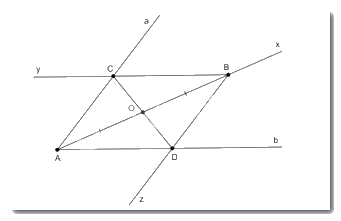
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.
Mục 2 của chương trình Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố các kiến thức về đa thức, phân thức đại số. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh thu gọn các đa thức đã cho bằng cách thực hiện các phép toán cộng, trừ, nhân, chia đa thức. Để thu gọn đa thức, học sinh cần thực hiện các bước sau:
Ví dụ: Thu gọn đa thức 3x2 + 2x - 5x2 + 7x - 1. Ta có:
3x2 + 2x - 5x2 + 7x - 1 = (3x2 - 5x2) + (2x + 7x) - 1 = -2x2 + 9x - 1
Bài tập này yêu cầu học sinh phân tích các đa thức đã cho thành nhân tử. Để phân tích đa thức thành nhân tử, học sinh có thể sử dụng các phương pháp sau:
Ví dụ: Phân tích đa thức x2 - 4 thành nhân tử. Ta có:
x2 - 4 = (x - 2)(x + 2)
Bài tập này yêu cầu học sinh tính giá trị của các biểu thức đại số khi biết giá trị của các biến. Để tính giá trị của biểu thức, học sinh cần thay các giá trị của các biến vào biểu thức và thực hiện các phép toán.
Ví dụ: Tính giá trị của biểu thức 2x + 3y khi x = 1 và y = 2. Ta có:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Bài tập này yêu cầu học sinh giải các phương trình đại số. Để giải phương trình, học sinh cần thực hiện các bước sau:
Ví dụ: Giải phương trình 2x + 5 = 11. Ta có:
2x + 5 = 11 => 2x = 6 => x = 3
Để học tốt môn Toán 8, các em cần thường xuyên luyện tập, làm bài tập và tìm hiểu các kiến thức mới. Ngoài ra, các em cũng nên tham gia các câu lạc bộ Toán học hoặc tìm kiếm sự giúp đỡ của các thầy cô giáo, bạn bè.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a - b)(a + b) | Hiệu hai bình phương |
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 59, 60, 61 SGK Toán 8 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!