Bài 9.16 trang 92 SGK Toán 8 tập 2 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.16, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình thang ABCD
Đề bài
Cho hình thang ABCD (AB // CD) và các điểm M, N lần lượt trên cạnh AD và BC sao cho 2AM=MD, 2BN=NC. Biết AB=5cm,CD=6cm. Hãy tính độ dài đoạn thẳng MN
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Gọi I là giao điểm của AC và MN
Sử dụng các tam giác đồng dạng để tính độ dài MI, IN. Từ đó tính độ dài đoạn MN.
Lời giải chi tiết
Gọi I là giao điểm của AC và MN
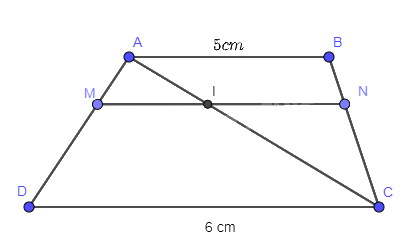
Vì 2AM=MD suy ra \(\frac{{AM}}{{M{\rm{D}}}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{A{\rm{D}}}} = \frac{1}{3}\)
Vì 2BN=NC suy ra \(\frac{{BN}}{{NC}} = \frac{1}{2} \Rightarrow \frac{{NC}}{{CB}} = \frac{2}{3}\)
Xét hình thang ABCD có \(\frac{{AM}}{{M{\rm{D}}}} = \frac{{BN}}{{NC}}\) suy ra MN // AB //DC
Xét hai tam giác AMI và ADC có: góc A chung, \(\widehat {AIM} = \widehat {AC{\rm{D}}}\) (do MN// DC)
Suy ra \(\Delta AMI \backsim \Delta A{\rm{D}}C\) suy ra: \(\frac{{AM}}{{{\rm{AD}}}} = \frac{{MI}}{{DC}} = \frac{1}{3} \Rightarrow MI = \frac{1}{3}.DC = \frac{1}{3}.6 = 2(cm)\)
Xét hai tam giác CNI và CBA có góc C chung, \(\widehat {CIN} = \widehat {CAB}\) (do MN // AB)
Suy ra \(\Delta CNI \backsim \Delta CBA\) suy ra: \(\frac{{CN}}{{CB}} = \frac{{NI}}{{BA}} = \frac{2}{3} \Rightarrow NI = \frac{2}{3}.BA = \frac{2}{3}.5 = \frac{{10}}{3}\)(cm)
MN = MI + IN = \(2 + \frac{{10}}{3} = \frac{{16}}{3}(cm)\)
Bài 9.16 trang 92 SGK Toán 8 tập 2 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài toán này, chúng ta cần nắm vững các khái niệm và tính chất của hàm số bậc nhất, cũng như cách xác định hệ số góc và tung độ gốc.
Bài toán 9.16 thường đưa ra một tình huống thực tế, ví dụ như mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa số lượng sản phẩm và giá thành. Nhiệm vụ của học sinh là xác định hàm số bậc nhất mô tả mối quan hệ đó.
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ, nếu bài toán liên quan đến quãng đường và thời gian, lời giải sẽ bao gồm việc xác định vận tốc (hệ số góc) và quãng đường ban đầu (tung độ gốc).)
Ví dụ:
Giả sử bài toán yêu cầu xác định hàm số biểu diễn quãng đường đi được của một ô tô với vận tốc 60km/h và đã đi được 20km ban đầu. Khi đó, hàm số sẽ có dạng:
y = 60x + 20
Trong đó:
Ngoài bài 9.16, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức, các em học sinh có thể tự giải các bài tập sau:
Bài 9.16 trang 92 SGK Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Bằng cách nắm vững lý thuyết và luyện tập thường xuyên, các em học sinh sẽ tự tin giải quyết các bài toán tương tự.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số góc | a, thể hiện độ dốc của đường thẳng |
| Tung độ gốc | b, giao điểm của đường thẳng với trục Oy |