Bài 4.3 trang 80 SGK Toán 8 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các định lý về hình bình hành và các tính chất liên quan. Bài tập này thường yêu cầu học sinh chứng minh một tính chất hoặc giải một bài toán thực tế liên quan đến hình bình hành.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.3 trang 80 SGK Toán 8 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho ∆ABC, từ điểm D trên cạnh BC,
Đề bài
Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh rằng: \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = 1\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thalès trong tam giác ABC, ta có các tỉ lệ thức. Áp dụng dãy tỉ số bằng nhau ta được đpcm.
Lời giải chi tiết
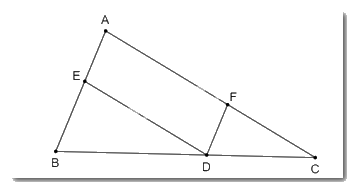
Áp dụng định lí Thalès, ta có:
• Vì DE // AC nên \(\dfrac{{A{\rm{E}}}}{{AB}} = \dfrac{{C{\rm{D}}}}{{BC}}\)
• Vì DF // AB nên \(\dfrac{{AF}}{{AC}} = \dfrac{{B{\rm{D}}}}{{BC}}\)
Khi đó, \(\dfrac{{A{\rm{E}}}}{{AB}} + \dfrac{{AF}}{{AC}} = \dfrac{{C{\rm{D}}}}{{BC}} + \dfrac{{B{\rm{D}}}}{{BC}} = 1\) (đpcm).
Bài 4.3 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hình bình hành, đặc biệt là các định lý liên quan đến tính chất đường chéo, góc và cạnh của hình bình hành. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và biết cách áp dụng chúng vào các bài toán cụ thể.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định hình bình hành nào được đề cập, các yếu tố nào đã cho và cần tìm gì. Việc phân tích đề bài giúp học sinh có cái nhìn tổng quan và lựa chọn phương pháp giải phù hợp.
(Nội dung lời giải chi tiết bài 4.3 sẽ được trình bày tại đây, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ:)
Bài 4.3: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng: a) F là trung điểm của AC; b) Tam giác ADF và tam giác CDE bằng nhau.
Giải:
Xét tam giác ABC, DE cắt AC tại F. Vì E là trung điểm của AB, ta có AE = EB. Áp dụng định lý Menelaus cho tam giác ABC với đường thẳng DE, ta có:
(AE/EB) * (BD/DC) * (CF/FA) = 1
Vì AE = EB và BD = DC (tính chất hình bình hành), nên:
(1) * (1) * (CF/FA) = 1
=> CF/FA = 1 => CF = FA. Vậy F là trung điểm của AC.
Xét tam giác ADF và tam giác CDE, ta có:
Vậy, tam giác ADF và tam giác CDE bằng nhau theo trường hợp góc - cạnh - góc (g-c-g).
Ngoài bài 4.3, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hình bình hành. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập này, học sinh cần:
Để nắm vững kiến thức về hình bình hành và rèn luyện kỹ năng giải bài tập, học sinh nên luyện tập thêm các bài tập trong SGK, sách bài tập và các nguồn tài liệu khác. Việc luyện tập thường xuyên giúp học sinh tự tin hơn khi làm bài kiểm tra và thi cử.
Bài 4.3 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình bình hành. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin giải các bài tập tương tự.