Bài 9.34 trang 109 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình hộp chữ nhật và hình lập phương vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.34 này, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cùng theo dõi bài giải dưới đây để hiểu rõ cách tiếp cận và giải quyết bài toán một cách hiệu quả nhất.
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao
Đề bài
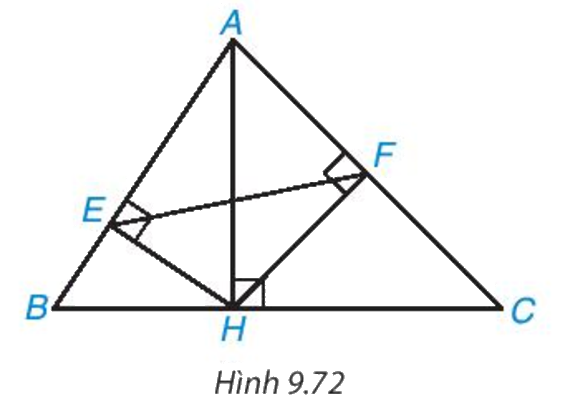
Trong hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng
a) ΔAEH ∽ ΔAHB
b) ΔAFH ∽ ΔAHC
c) ΔAFE ∽ ΔABC
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các trường hợp đồng dạng của tam giác vuông và tam giác thường.
Lời giải chi tiết
a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có: góc A chung
=> ΔAEH ∽ ΔAHB
b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có: góc A chung
ΔAFH ∽ ΔAHC
c) Vì ΔAEH ∽ ΔAHB nên:
\(\frac{{A{\rm{E}}}}{{AH}} = \frac{{AH}}{{AB}} \Rightarrow A{\rm{E}} = \frac{{A{H^2}}}{{AB}}\) (1)
Vì ΔAFH ∽ ΔAHC nên:
\(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}} \Rightarrow AF = \frac{{A{H^2}}}{{AC}}\)(2)
Từ (1) và (2) ta có:
\(\frac{{A{\rm{E}}}}{{AF}} = \frac{{AC}}{{AB}} \Rightarrow \frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\)
Xét hai tam giác ΔAFE và ΔABC có:
Góc A chung
\(\frac{{AF}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}}\)
Suy ra ΔAFE ∽ ΔABC (c.g.c)
Bài 9.34 trang 109 SGK Toán 8 tập 2 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về thể tích hình hộp chữ nhật và hình lập phương để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tính toán thể tích của các vật thể có hình dạng tương tự, hoặc so sánh thể tích của các vật thể khác nhau.
Để hiểu rõ hơn về bài toán, chúng ta cần xem xét nội dung cụ thể của nó. Thông thường, bài toán sẽ cung cấp các thông tin về kích thước của hình hộp chữ nhật hoặc hình lập phương, chẳng hạn như chiều dài, chiều rộng, chiều cao. Dựa vào các thông tin này, học sinh cần áp dụng công thức tính thể tích để tìm ra đáp án.
Trước khi đi vào giải bài toán, chúng ta cần ôn lại công thức tính thể tích của hình hộp chữ nhật và hình lập phương:
Để giải bài 9.34 trang 109 SGK Toán 8 tập 2 - Kết nối tri thức một cách hiệu quả, học sinh có thể áp dụng các bước sau:
Giả sử bài toán 9.34 yêu cầu tính thể tích của một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Ta sẽ áp dụng công thức tính thể tích hình hộp chữ nhật:
V = a * b * c = 5cm * 3cm * 4cm = 60cm3
Vậy thể tích của hình hộp chữ nhật là 60cm3.
Việc giải bài 9.34 trang 109 SGK Toán 8 tập 2 - Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về thể tích hình hộp chữ nhật và hình lập phương, mà còn có ứng dụng thực tế cao trong cuộc sống. Ví dụ, chúng ta có thể sử dụng kiến thức này để tính toán lượng nước cần thiết để đổ đầy một bể bơi, hoặc tính toán lượng vật liệu cần thiết để xây dựng một ngôi nhà.
Bài 9.34 trang 109 SGK Toán 8 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán và áp dụng kiến thức vào thực tế. Bằng cách nắm vững công thức tính thể tích và áp dụng phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài toán và đạt kết quả tốt trong các bài kiểm tra.