Bài 9.19 trang 97 SGK Toán 8 tập 2 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Tính độ dài x, y, z, t trong Hình 9.43
Đề bài
Tính các độ dài x, y, z, t trong Hình 9.43
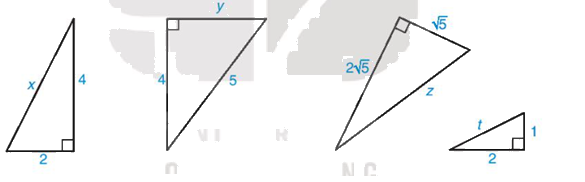
Hình 9.43
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore trong tam giác vuông
Lời giải chi tiết
\({x^2} = {4^2} + {2^2} = 20 \) suy ra \( x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \) suy ra \( y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \) suy ra \( z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \) suy ra \( t = \sqrt 5 \)
Bài 9.19 SGK Toán 8 tập 2 yêu cầu chúng ta giải một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài này, trước tiên chúng ta cần hiểu rõ định nghĩa và các tính chất của hàm số bậc nhất. Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a khác 0.
Đề bài thường mô tả một tình huống cụ thể, ví dụ như mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa số lượng sản phẩm và doanh thu. Nhiệm vụ của chúng ta là xác định hàm số bậc nhất mô tả mối quan hệ đó và sử dụng hàm số để trả lời các câu hỏi của đề bài.
Giả sử đề bài: Một chiếc xe ô tô đi từ A đến B với vận tốc không đổi là 60km/h. Gọi t là thời gian xe đi (tính bằng giờ) và s là quãng đường xe đi được (tính bằng km). Hãy viết công thức tính quãng đường s theo thời gian t.
Giải:
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể giải thêm các bài tập tương tự trong SGK Toán 8 tập 2 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 9.19 trang 97 SGK Toán 8 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Bằng cách nắm vững các bước giải và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài toán tương tự.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, với a ≠ 0 |
| Hệ số a | Xác định độ dốc của đường thẳng biểu diễn hàm số |
| Hệ số b | Xác định giao điểm của đường thẳng với trục tung |