Bài 9.9 trang 90 SGK Toán 8 tập 2 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng định lý về tổng các góc trong một tứ giác. Bài tập này thường gây khó khăn cho học sinh do yêu cầu phân tích hình vẽ và vận dụng kiến thức đã học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.9 trang 90 SGK Toán 8 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC
Đề bài
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)
a) Chứng minh rằng ΔABN ∽ ΔACM
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh: tam giác ABN và tam giác ACM
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM
b) Chứng minh: ΔIBM ∽ ΔICN (g.g) nên suy ra các tỉ số đồng dạng
Lời giải chi tiết
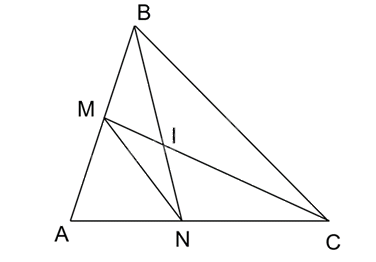
a) Xét tam giác ABN và tam giác ACM
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM (g.g)
b) Có ΔABN ∽ ΔACM
\(\widehat {ANB} = \widehat {AMC}\)
Có \(\widehat {ANB} + \widehat {CNB} = {180^o}\)
\(\widehat {AMC} + \widehat {BMC} = {180^o}\)
=> \(\widehat {CNB} = \widehat {BMC}\)
Xét tam giác IBM và tam giác ICN
Có \(\widehat {CNB} = \widehat {BMC}\) và \(\widehat {IBM} = \widehat {ICN}\)
=> ΔIBM ∽ ΔICN (g.g)
=> \(\frac{{IB}}{{IC}} = \frac{{IM}}{{IN}}\)
=> IB.IN=IC.IM
Bài 9.9 trang 90 SGK Toán 8 tập 2 yêu cầu chúng ta giải quyết một bài toán liên quan đến tứ giác và tổng các góc trong tứ giác. Để giải bài này một cách hiệu quả, chúng ta cần nắm vững định lý về tổng các góc trong một tứ giác, đó là tổng bốn góc của một tứ giác luôn bằng 360 độ.
Cho tứ giác ABCD. Biết số đo các góc A, B, C lần lượt là 65o, 75o, 100o. Tính số đo góc D.
Áp dụng định lý về tổng các góc trong một tứ giác, ta có:
∠A + ∠B + ∠C + ∠D = 360o
Thay số đo các góc A, B, C đã cho vào, ta được:
65o + 75o + 100o + ∠D = 360o
240o + ∠D = 360o
∠D = 360o - 240o
∠D = 120o
Vậy số đo góc D của tứ giác ABCD là 120o.
Bài toán này là một ví dụ điển hình về việc áp dụng định lý về tổng các góc trong một tứ giác. Để giải các bài toán tương tự, chúng ta cần:
Để củng cố kiến thức về tổng các góc trong một tứ giác, các em có thể luyện tập thêm các bài tập sau:
Ngoài định lý về tổng các góc trong một tứ giác, chúng ta còn có các định lý khác liên quan đến tứ giác, như:
Việc nắm vững các định lý này sẽ giúp chúng ta giải quyết các bài toán về tứ giác một cách dễ dàng và hiệu quả hơn.
Khi giải bài tập về tứ giác, các em nên:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 9.9 trang 90 SGK Toán 8 tập 2 - Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.