Bài 3.35 trang 73 SGK Toán 8 tập 1 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.35 trang 73 SGK Toán 8 tập 1 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Cho hình bình hành ABCD.
Đề bài
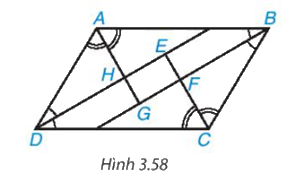
Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh tứ giác EFGH là hình bình hành có \(\widehat {EHG} = {90^o};\widehat {AGF} = {90^o};\widehat {{\rm{HEF}}} = {90^o}\) nên tứ giác EFGH là hình chữ nhật.
Lời giải chi tiết
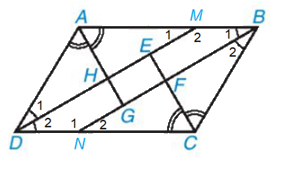
Vì tứ giác ABCD là hình bình hành nên AB // CD hay AM // DN.
Suy ra \(\widehat {{M_1}} = \widehat {{D_2}}\)(hai góc so le trong)
Mà \(\widehat {{D_1}} = \widehat {{D_2}}\) (vì DM là tia phân giác \(\widehat {A{\rm{D}}C}\)).
Do đó \(\widehat {{M_1}} = \widehat {{D_1}}\) nên tam giác ADM cân tại A.
Chứng minh tương tự, ta có tam giác BCN cân tại C.
Vì \(\widehat {{B_1}} = \widehat {{B_2}};\widehat {{D_1}} = \widehat {{D_2}}\) (vì DM, BN lần lượt là tia phân giác của \(\widehat {A{\rm{D}}C};\widehat {ABC}\)).
Mà \(\widehat {A{\rm{D}}C} = \widehat {ABC}\) (vì tứ giác ABCD là hình bình hành).
Do đó \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\)
Tam giác ADM cân tại A, tam giác BCN cân tại C.
Mà \(\widehat {{B_1}} = \widehat {{D_2}}\) nên \(\widehat {{M_1}} = \widehat {{N_2}}\) suy ra \(\widehat {{M_2}} = \widehat {{N_1}}\)
Tứ giác BMDN có \(\widehat {{B_1}} = \widehat {{D_2}};\widehat {{M_2}} = \widehat {{N_1}}\) nên tứ giác BMDN là hình bình hành.
Suy ra DM // BN hay HE // GF.
Tam giác ADM cân tại A có AH là đường phân giác nên AH cũng là đường cao.
Suy ra \(\widehat {AHE} = {90^o}\) nên \(\widehat {EHG} = {90^o}\)
Mà HE // GF suy ra \(\widehat {AGF} = {90^o}\) (hai góc đồng vị).
Tương tự, ta cũng chứng minh được: \(\widehat {HEF} = {90^o};\widehat {GF{\rm{E}}} = {90^o}\)
Tứ giác EFGH có \(\widehat {EHG} = {90^o};\widehat {AGF} = {90^o};\widehat {{\rm{HEF}}} = {90^o}\)
Do đó tứ giác EFGH là hình chữ nhật.
Bài 3.35 trang 73 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của các góc so le trong, đồng vị, trong cùng phía.
Cho hình vẽ sau (hình vẽ minh họa bài 3.35 trang 73 SGK Toán 8 tập 1 - Kết nối tri thức). Biết rằng a // b. Tìm số đo của các góc còn lại trên hình.
Để giải bài tập này, chúng ta sẽ sử dụng các tính chất của các góc tạo bởi một đường thẳng cắt hai đường thẳng song song:
Bước 1: Xác định các góc đã biết.
Giả sử góc A1 = 60 độ (ví dụ). Từ đó, ta có thể suy ra các góc khác dựa trên các tính chất đã nêu.
Bước 2: Sử dụng tính chất góc so le trong.
Nếu góc A1 và góc B1 là góc so le trong, thì góc B1 = góc A1 = 60 độ.
Bước 3: Sử dụng tính chất góc đồng vị.
Nếu góc A1 và góc B2 là góc đồng vị, thì góc B2 = góc A1 = 60 độ.
Bước 4: Sử dụng tính chất góc trong cùng phía.
Nếu góc A1 và góc B3 là góc trong cùng phía, thì góc A1 + góc B3 = 180 độ. Suy ra, góc B3 = 180 độ - góc A1 = 180 độ - 60 độ = 120 độ.
Bước 5: Tiếp tục suy luận để tìm các góc còn lại.
Sử dụng các tính chất tương tự, ta có thể tìm được số đo của tất cả các góc còn lại trên hình.
Giả sử góc A1 = 70 độ. Hãy tìm số đo của các góc còn lại.
Khi giải bài tập này, học sinh cần chú ý:
Để rèn luyện kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng, học sinh có thể làm thêm các bài tập tương tự trong SGK Toán 8 tập 1 - Kết nối tri thức.
Bài 3.35 trang 73 SGK Toán 8 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ giải bài tập này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!