Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 53, 54 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, chính xác, cùng với phương pháp giải dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và phù hợp với chương trình học hiện hành. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
Video hướng dẫn giải
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
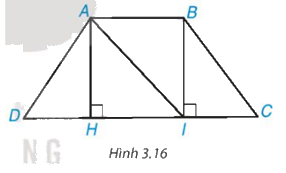
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC
Phương pháp giải:
a) Chứng minh: ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Chứng minh: ∆AHD = ∆BIC (góc - góc).
Suy ra AD = BC (hai cạnh tương ứng).
Lời giải chi tiết:
a) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat {BAI} = \widehat {AIH}\) (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó \(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
\(\widehat {BAI} = \widehat {AIH}\) (chứng minh trên);
Cạnh AI chung;
\(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Do đó ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat C = \widehat D\).
Vì ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) và \(\widehat C = \widehat D\) nên \(90^o - \widehat C = 90^o - \widehat {BIC} \Leftrightarrow \widehat {DAH} = \widehat {CBI}\)
Xét ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
\(AH = BI\) (chứng minh trên
\(\widehat {DAH} = \widehat {CBI}\) (chứng minh trên).
Do đó ∆AHD = ∆BIC (góc - cạnh - góc).
Suy ra AD = BC (hai cạnh tương ứng).
Video hướng dẫn giải
Cho tứ giác ABCD như Hình 3.18. Biết rằng \(\widehat A = \widehat B = \widehat {{D_1}}\). Chứng minh rằng AD = BC.
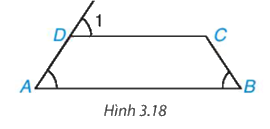
Phương pháp giải:
Chứng minh ABCD là hình thang có \(\widehat A = \widehat B\)
Lời giải chi tiết:
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).
Video hướng dẫn giải
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
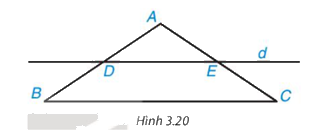
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Phương pháp giải:
Sử dụng tính chất của hình thang cân.
Lời giải chi tiết:
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C\).
Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
Video hướng dẫn giải
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
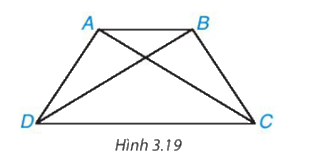
Phương pháp giải:
Chứng minh:∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Lời giải chi tiết:
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Video hướng dẫn giải
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
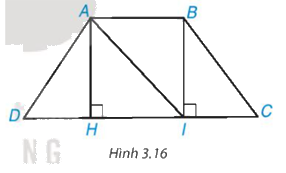
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC
Phương pháp giải:
a) Chứng minh: ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Chứng minh: ∆AHD = ∆BIC (góc - góc).
Suy ra AD = BC (hai cạnh tương ứng).
Lời giải chi tiết:
a) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat {BAI} = \widehat {AIH}\) (hai góc so le trong).
Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.
Do đó \(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Xét ∆AHI và ∆IBA có:
\(\widehat {BAI} = \widehat {AIH}\) (chứng minh trên);
Cạnh AI chung;
\(\widehat {AIB} = \widehat {HAI}\) (hai góc so le trong).
Do đó ∆AHI = ∆IBA (g.c.g).
Suy ra AH = BI (hai cạnh tương ứng).
b) Vì ABCD là hình thang cân (AB // CD) nên \(\widehat C = \widehat D\).
Vì ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) và \(\widehat C = \widehat D\) nên \(90^o - \widehat C = 90^o - \widehat {BIC} \Leftrightarrow \widehat {DAH} = \widehat {CBI}\)
Xét ∆AHD và ∆BIC có:
\(\widehat {AH{\rm{D}}} = \widehat {BIC} = {90^o}\) (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
\(AH = BI\) (chứng minh trên
\(\widehat {DAH} = \widehat {CBI}\) (chứng minh trên).
Do đó ∆AHD = ∆BIC (góc - cạnh - góc).
Suy ra AD = BC (hai cạnh tương ứng).
Video hướng dẫn giải
Cho tứ giác ABCD như Hình 3.18. Biết rằng \(\widehat A = \widehat B = \widehat {{D_1}}\). Chứng minh rằng AD = BC.
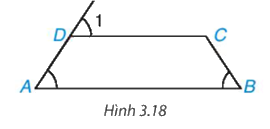
Phương pháp giải:
Chứng minh ABCD là hình thang có \(\widehat A = \widehat B\)
Lời giải chi tiết:
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).
Video hướng dẫn giải
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
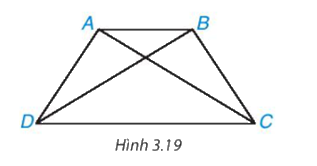
Phương pháp giải:
Chứng minh:∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Lời giải chi tiết:
Vì ABCD là hình thang cân (AC // CD) nên AD = BC; \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)
Xét ∆ACD và ∆BDC có
AD = BC (chứng minh trên);
\(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\) (chứng minh trên);
Cạnh CD chung.
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra AC = BD (hai góc tương ứng).
Video hướng dẫn giải
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
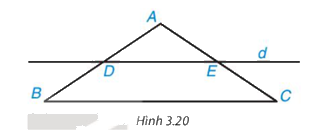
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Phương pháp giải:
Sử dụng tính chất của hình thang cân.
Lời giải chi tiết:
a) Theo đề bài: d // BC nên DE // BC
Suy ra DECB là hình thang.
Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C\).
Hình thang DECB có \(\widehat B = \widehat C\) nên tứ giác DECB là hình thang cân.
b) Hình thang cân DECB có BE và CD là hai đường chéo.
Do đó BE = CD (đpcm).
Mục 2 trang 53, 54 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Nội dung chính bao gồm việc thu gọn đa thức, xác định bậc của đa thức, và thực hiện các phép cộng, trừ đa thức. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các bài học tiếp theo trong chương trình Toán 8.
Để thu gọn đa thức, ta cần thực hiện các bước sau:
Bậc của đa thức là bậc cao nhất của các hạng tử trong đa thức đó.
Để cộng hoặc trừ hai đa thức, ta thực hiện các bước sau:
Bài 1: Thu gọn đa thức sau: A = 3x2 + 2xy - x2 + 5xy - 2x2
Lời giải:
A = (3x2 - x2 - 2x2) + (2xy + 5xy)
A = 0x2 + 7xy
A = 7xy
Bài 2: Tính (2x2 - 3x + 1) + (x2 + 2x - 3)
Lời giải:
(2x2 - 3x + 1) + (x2 + 2x - 3) = (2x2 + x2) + (-3x + 2x) + (1 - 3)
= 3x2 - x - 2
Ngoài các dạng bài tập cơ bản về thu gọn đa thức và cộng trừ đa thức, học sinh còn có thể gặp các dạng bài tập phức tạp hơn như:
Để giải quyết các dạng bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đa thức và rèn luyện kỹ năng biến đổi đại số.
Để học tốt môn Toán 8, đặc biệt là phần đại số, học sinh cần:
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn khi giải các bài tập về đa thức trong chương trình Toán 8 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!