Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 2 trang 70, 71 sách giáo khoa Toán 8 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết, giúp các em tự tin hơn trong quá trình học tập và ôn luyện môn Toán.
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Video hướng dẫn giải
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Phương pháp giải:
Dựa vào tính chất: hình vuông cũng là hình thoi và hình chữ nhật
Lời giải chi tiết:
Hình vuông cũng là hình thoi, hình chữ nhật.
Mà hình chữ nhật có hai đường chéo bằng nhau còn hình thoi có hai đường chéo vuông góc với nhau.
Do đó, hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
Phương pháp giải:
Vẽ hình và ghi giả thiết kết luận theo hình
Lời giải chi tiết:
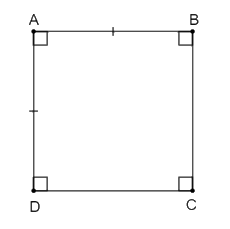
GT | Hình chữ nhật ABCD có AB = AD. |
KL | ABCD là hình vuông. |
Ta có thể viết giả thiết đối với cặp cạnh kề khác như: AB = BC; BC = CD; CD = AD.
Video hướng dẫn giải
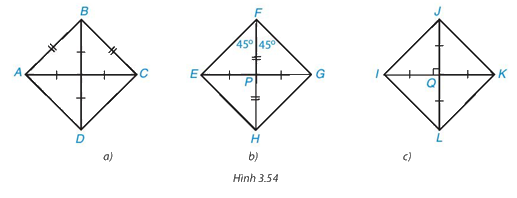
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
Phương pháp giải:
Dựa vào các dấu hiệu nhận biết hình vuông
Lời giải chi tiết:
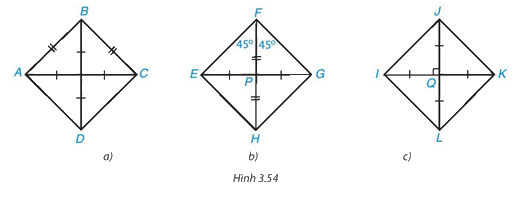
• Hình 3.54a)
Tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác này là hình chữ nhật.
Mà AB = BC nên tứ giác ABCD là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình 3.54b)
Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm P của mỗi đường.
Ta có \[\widehat {EFG} = \widehat {EFP} + \widehat {GFP} = {45^o} + {45^o} = {90^o}\]
Suy ra tứ giác EFGH là hình chữ nhật.
Hình chữ nhật EFGH có đường chéo FH là đường phân giác của \(\widehat {EFG}\).
Do đó tứ giác EFGH là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.
• Hình 3.54c)
Tứ giác IJKL có hai đường chéo IK và JL bằng nhau và cắt nhau tại trung điểm Q của mỗi đường.
Suy ra tứ giác IJKL là hình chữ nhật.
Mà IK ⊥ JL nên tứ giác IJKL là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình vuông
Video hướng dẫn giải
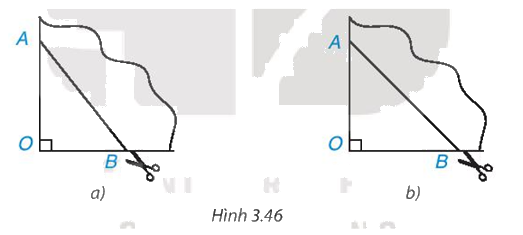
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
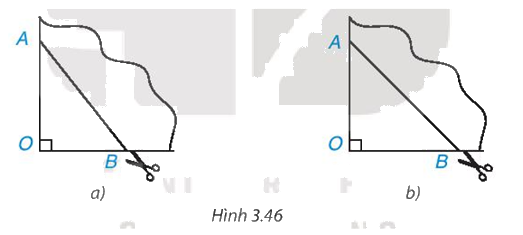
Hãy giải thích tại sao.
- Trong trường hợp a, ta được hình thoi.
- Trong trường hợp b, ta được hình vuông
Phương pháp giải:
Quan sát hình 3.46 và giải thích
Lời giải chi tiết:
- Trong trường hợp a:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
Video hướng dẫn giải
Hãy giải thích tại sao hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Phương pháp giải:
Dựa vào tính chất: hình vuông cũng là hình thoi và hình chữ nhật
Lời giải chi tiết:
Hình vuông cũng là hình thoi, hình chữ nhật.
Mà hình chữ nhật có hai đường chéo bằng nhau còn hình thoi có hai đường chéo vuông góc với nhau.
Do đó, hai đường chéo của hình vuông bằng nhau và vuông góc với nhau.
Video hướng dẫn giải
Hãy viết giả thiết, kết luận của câu a trong Định lí 4.
Phương pháp giải:
Vẽ hình và ghi giả thiết kết luận theo hình
Lời giải chi tiết:
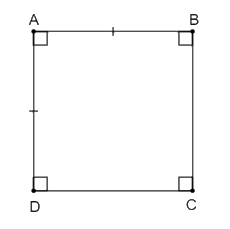
GT | Hình chữ nhật ABCD có AB = AD. |
KL | ABCD là hình vuông. |
Ta có thể viết giả thiết đối với cặp cạnh kề khác như: AB = BC; BC = CD; CD = AD.
Video hướng dẫn giải
Với mỗi hình dưới đây, ta dùng dấu hiệu nhận biết nào để khẳng định đó là hình vuông?
Phương pháp giải:
Dựa vào các dấu hiệu nhận biết hình vuông
Lời giải chi tiết:
• Hình 3.54a)
Tứ giác ABCD có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra tứ giác này là hình chữ nhật.
Mà AB = BC nên tứ giác ABCD là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
• Hình 3.54b)
Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm P của mỗi đường.
Ta có \[\widehat {EFG} = \widehat {EFP} + \widehat {GFP} = {45^o} + {45^o} = {90^o}\]
Suy ra tứ giác EFGH là hình chữ nhật.
Hình chữ nhật EFGH có đường chéo FH là đường phân giác của \(\widehat {EFG}\).
Do đó tứ giác EFGH là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có một đường chéo là đường phân giác của một góc của hình vuông.
• Hình 3.54c)
Tứ giác IJKL có hai đường chéo IK và JL bằng nhau và cắt nhau tại trung điểm Q của mỗi đường.
Suy ra tứ giác IJKL là hình chữ nhật.
Mà IK ⊥ JL nên tứ giác IJKL là hình vuông.
Ta dùng dấu hiệu nhận biết: Hình chữ nhật có hai đường chéo vuông góc là hình vuông
Video hướng dẫn giải
Lấy một tờ giấy, gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông rồi cắt theo đoạn thẳng AB (H.3.46a). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác đó là hình gì? Vì sao? Nếu ta có OA = OB thì tứ giác nhận được là hình gì (H.3.46b)?
Hãy giải thích tại sao.
- Trong trường hợp a, ta được hình thoi.
- Trong trường hợp b, ta được hình vuông
Phương pháp giải:
Quan sát hình 3.46 và giải thích
Lời giải chi tiết:
- Trong trường hợp a:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông thì tạo ra tứ giác có bốn cạnh bằng nhau và đều bằng cạnh AB.
Khi đó, tứ giác ABCD là hình thoi.
- Trong trường hợp b:
Khi gấp làm tư tạo ra một góc vuông O, đánh dấu hai điểm A, B trên hai cạnh góc vuông. Nếu OA = OB thì hai đường chéo của tứ giác bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
Khi đó, tứ giác đã cho là hình vuông.
Mục 2 của chương trình Toán 8 tập 1 Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về các phép biến đổi đơn giản với đa thức. Nội dung chính bao gồm các bài tập về thu gọn đa thức, tìm bậc của đa thức, và thực hiện các phép cộng, trừ, nhân đa thức. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Bài 1 yêu cầu học sinh thu gọn các đa thức đã cho. Để thu gọn đa thức, ta cần thực hiện các phép cộng, trừ các đơn thức đồng dạng. Ví dụ, để thu gọn đa thức 3x2 + 2x - x2 + 5x, ta cộng các đơn thức đồng dạng 3x2 và -x2, và 2x và 5x. Kết quả là 2x2 + 7x.
Bài 2 yêu cầu học sinh tìm bậc của các đa thức đã cho. Bậc của đa thức là bậc của đơn thức có bậc cao nhất trong đa thức đó. Ví dụ, đa thức 2x3 + 5x2 - x + 1 có bậc là 3.
Bài 3 yêu cầu học sinh thực hiện các phép cộng, trừ đa thức. Để cộng hoặc trừ hai đa thức, ta cộng hoặc trừ các đơn thức đồng dạng tương ứng. Ví dụ, để cộng hai đa thức (3x2 + 2x - 1) và (x2 - 5x + 2), ta cộng các đơn thức đồng dạng 3x2 và x2, 2x và -5x, và -1 và 2. Kết quả là 4x2 - 3x + 1.
Bài 4 yêu cầu học sinh thực hiện phép nhân đa thức. Để nhân hai đa thức, ta sử dụng tính chất phân phối của phép nhân đối với phép cộng. Ví dụ, để nhân hai đa thức (x + 2) và (x - 3), ta thực hiện như sau:
Ví dụ 1: Thu gọn đa thức: 5x2y - 3xy2 + 2x2y + xy2
Giải: 5x2y - 3xy2 + 2x2y + xy2 = (5x2y + 2x2y) + (-3xy2 + xy2) = 7x2y - 2xy2
Ví dụ 2: Tìm bậc của đa thức: 4x3 - 2x2 + x - 5
Giải: Bậc của đa thức là 3.
Việc giải các bài tập trong mục 2 trang 70, 71 SGK Toán 8 tập 1 - Kết nối tri thức đòi hỏi học sinh phải nắm vững các kiến thức cơ bản về đa thức và các phép toán trên đa thức. Bằng cách luyện tập thường xuyên và áp dụng các phương pháp giải bài tập hiệu quả, các em sẽ đạt được kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| A + B = B + A | Tính giao hoán của phép cộng |
| A * B = B * A | Tính giao hoán của phép nhân |
| A * (B + C) = A * B + A * C | Tính chất phân phối của phép nhân đối với phép cộng |