Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học một cách nhanh chóng và hiệu quả nhất. Bài giải của chúng tôi không chỉ cung cấp đáp án mà còn đi kèm với các bước giải thích chi tiết, giúp bạn hiểu rõ bản chất của vấn đề.
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D. Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số (dfrac{{DB}}{{DC}}) và (dfrac{{AB}}{{AC}})
Video hướng dẫn giải
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D
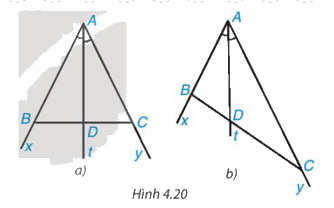
Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Phương pháp giải:
Dùng thước đo các khoảng cách và tính tỉ số
Lời giải chi tiết:
Dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC, ta được:
DB = 12 mm = 1,2 cm và DC = 24 mm = 2,4 cm.
Khi đó, \(\dfrac{{DB}}{{DC}} = \dfrac{{1,2}}{{2,4}} = \dfrac{1}{2};\dfrac{{AB}}{{AC}} = \dfrac{2}{4} = \dfrac{1}{2}\)
Vậy khi lấy B và C sao cho AB = 2 cm và AC = 4 cm thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Video hướng dẫn giải
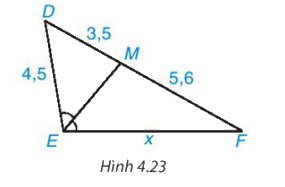
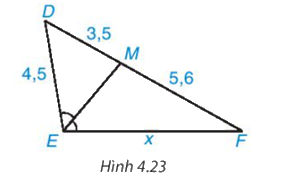
Tính độ dài x trên Hình 4.23
Phương pháp giải:
Vận dụng tính chất đường phân giác trong tam giác
Lời giải chi tiết:
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).
Video hướng dẫn giải
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.
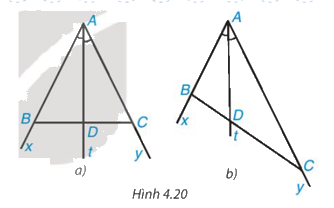
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Phương pháp giải:
Vận dụng tính chất đường phân giác của tam giác.
Lời giải chi tiết:
Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.
Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC.
Suy ra D là trung điểm của cạnh BC hay DB = DC nên \(\dfrac{{DB}}{{DC}} = 1\).
Vì AB = AC nên \(\dfrac{{AB}}{{AC}} = 1\)
Vậy khi lấy B và C sao cho AB = AC thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Video hướng dẫn giải
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.
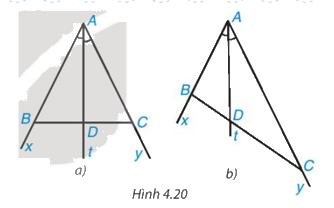
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Phương pháp giải:
Vận dụng tính chất đường phân giác của tam giác.
Lời giải chi tiết:
Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.
Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC.
Suy ra D là trung điểm của cạnh BC hay DB = DC nên \(\dfrac{{DB}}{{DC}} = 1\).
Vì AB = AC nên \(\dfrac{{AB}}{{AC}} = 1\)
Vậy khi lấy B và C sao cho AB = AC thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Video hướng dẫn giải
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D
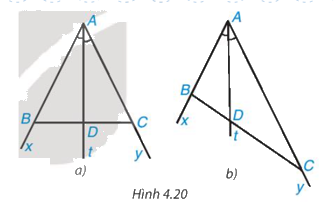
Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Phương pháp giải:
Dùng thước đo các khoảng cách và tính tỉ số
Lời giải chi tiết:
Dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC, ta được:
DB = 12 mm = 1,2 cm và DC = 24 mm = 2,4 cm.
Khi đó, \(\dfrac{{DB}}{{DC}} = \dfrac{{1,2}}{{2,4}} = \dfrac{1}{2};\dfrac{{AB}}{{AC}} = \dfrac{2}{4} = \dfrac{1}{2}\)
Vậy khi lấy B và C sao cho AB = 2 cm và AC = 4 cm thì \(\dfrac{{DB}}{{DC}} = \dfrac{{AB}}{{AC}}\)
Video hướng dẫn giải
Tính độ dài x trên Hình 4.23
Phương pháp giải:
Vận dụng tính chất đường phân giác trong tam giác
Lời giải chi tiết:
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).
Trang 84 và 85 SGK Toán 8 tập 1 - Kết nối tri thức tập trung vào các bài tập liên quan đến các kiến thức đã học trong chương. Các bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các vấn đề thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là rất quan trọng để hoàn thành tốt các bài tập này.
Trang 84 SGK Toán 8 tập 1 - Kết nối tri thức thường bao gồm các bài tập về:
Trang 85 SGK Toán 8 tập 1 - Kết nối tri thức thường bao gồm các bài tập về:
Để giải tốt các bài tập trang 84, 85 SGK Toán 8 tập 1 - Kết nối tri thức, bạn cần:
Ví dụ: Cho hình vẽ, biết AB // CD. Tính số đo góc BDC.
Giải:
Vì AB // CD nên góc BAC = góc ACD (so le trong). Mà góc BAC = 60 độ nên góc ACD = 60 độ. Trong tam giác ACD, ta có: góc ADC + góc ACD + góc CAD = 180 độ. Suy ra: góc ADC = 180 độ - 60 độ - 70 độ = 50 độ. Vậy góc BDC = 50 độ.
Khi giải bài tập, bạn cần chú ý:
Giaitoan.edu.vn cung cấp:
Hy vọng với những hướng dẫn chi tiết và lời giải bài tập trên, bạn sẽ tự tin hơn trong việc học Toán 8 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!