Chào mừng bạn đến với bài học về Lý thuyết Tổng và Hiệu hai Lập phương trong chương trình Toán 8 - Kết nối tri thức tại giaitoan.edu.vn. Đây là một trong những kiến thức quan trọng giúp bạn giải quyết các bài toán đại số một cách hiệu quả.
Bài học này sẽ cung cấp cho bạn những khái niệm cơ bản, công thức quan trọng và các ví dụ minh họa giúp bạn hiểu rõ về tổng và hiệu hai lập phương.
Tổng hai lập phương là gì?
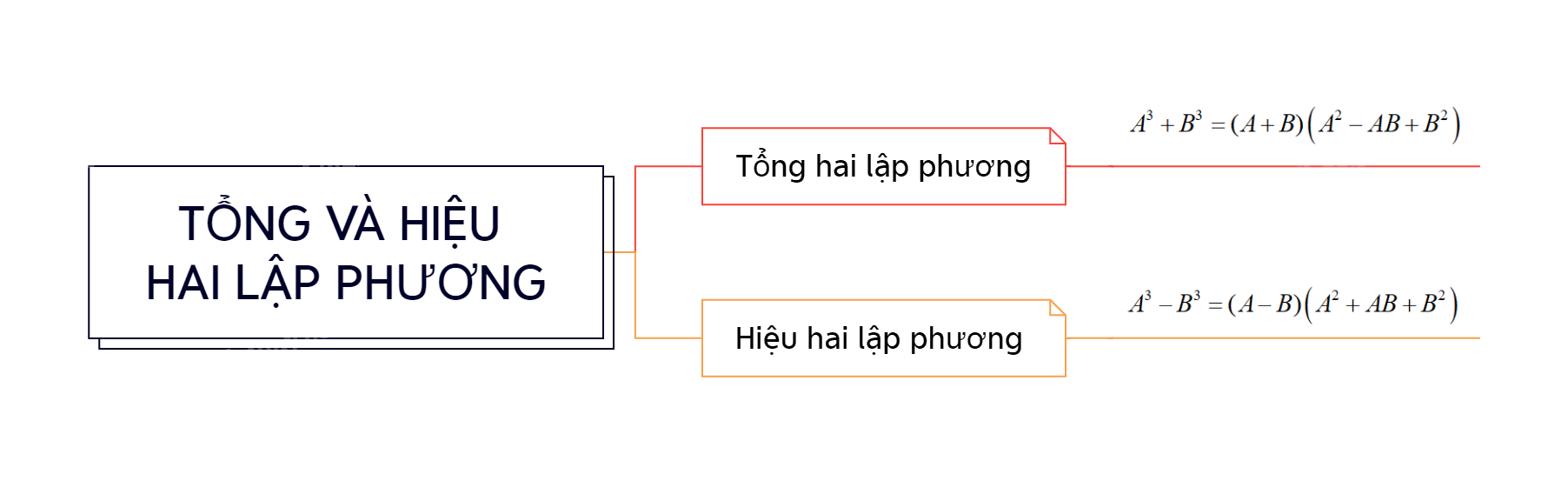
Tổng hai lập phương
\({A^3} + {B^3} = (A + B)\left( {{A^2} - AB + {B^2}} \right)\)
Ví dụ: \({x^3} + 8 = {x^3} + {2^3} = (x + 2)({x^2} - 2x + 4)\)
+ Hiệu hai lập phương
\({A^3} - {B^3} = (A - B)\left( {{A^2} + AB + {B^2}} \right)\)
Ví dụ: \({x^3} - 8 = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\)
Trong chương trình Toán 8, phần đại số đóng vai trò quan trọng trong việc xây dựng nền tảng toán học vững chắc. Một trong những kiến thức không thể bỏ qua là Lý thuyết Tổng và Hiệu hai Lập phương. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, cùng với các ví dụ minh họa và bài tập vận dụng để giúp bạn nắm vững kiến thức.
Công thức tổng hai lập phương được biểu diễn như sau:
a3 + b3 = (a + b)(a2 - ab + b2)
Trong đó:
Ví dụ:
Tính 23 + 33
Áp dụng công thức, ta có:
23 + 33 = (2 + 3)(22 - 2*3 + 32) = 5(4 - 6 + 9) = 5 * 7 = 35
Công thức hiệu hai lập phương được biểu diễn như sau:
a3 - b3 = (a - b)(a2 + ab + b2)
Trong đó:
Ví dụ:
Tính 53 - 23
Áp dụng công thức, ta có:
53 - 23 = (5 - 2)(52 + 5*2 + 22) = 3(25 + 10 + 4) = 3 * 39 = 117
Lý thuyết Tổng và Hiệu hai Lập phương có nhiều ứng dụng trong việc giải các bài toán đại số, đặc biệt là:
Dưới đây là một số bài tập vận dụng để bạn luyện tập và củng cố kiến thức:
Hướng dẫn giải:
Khi áp dụng công thức Tổng và Hiệu hai Lập phương, bạn cần lưu ý:
Hy vọng bài viết này đã giúp bạn hiểu rõ về Lý thuyết Tổng và Hiệu hai Lập phương trong chương trình Toán 8 - Kết nối tri thức. Chúc bạn học tập tốt!