Chào mừng bạn đến với bài học về lý thuyết Tính chất cơ bản của phân thức đại số trong chương trình Toán 8 - Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về phân thức đại số, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa phân thức đại số, các tính chất cơ bản như tính chất bằng nhau của hai phân thức, quy tắc đổi dấu, và các phép toán trên phân thức.
Tính chất cơ bản của phân thức là gì?
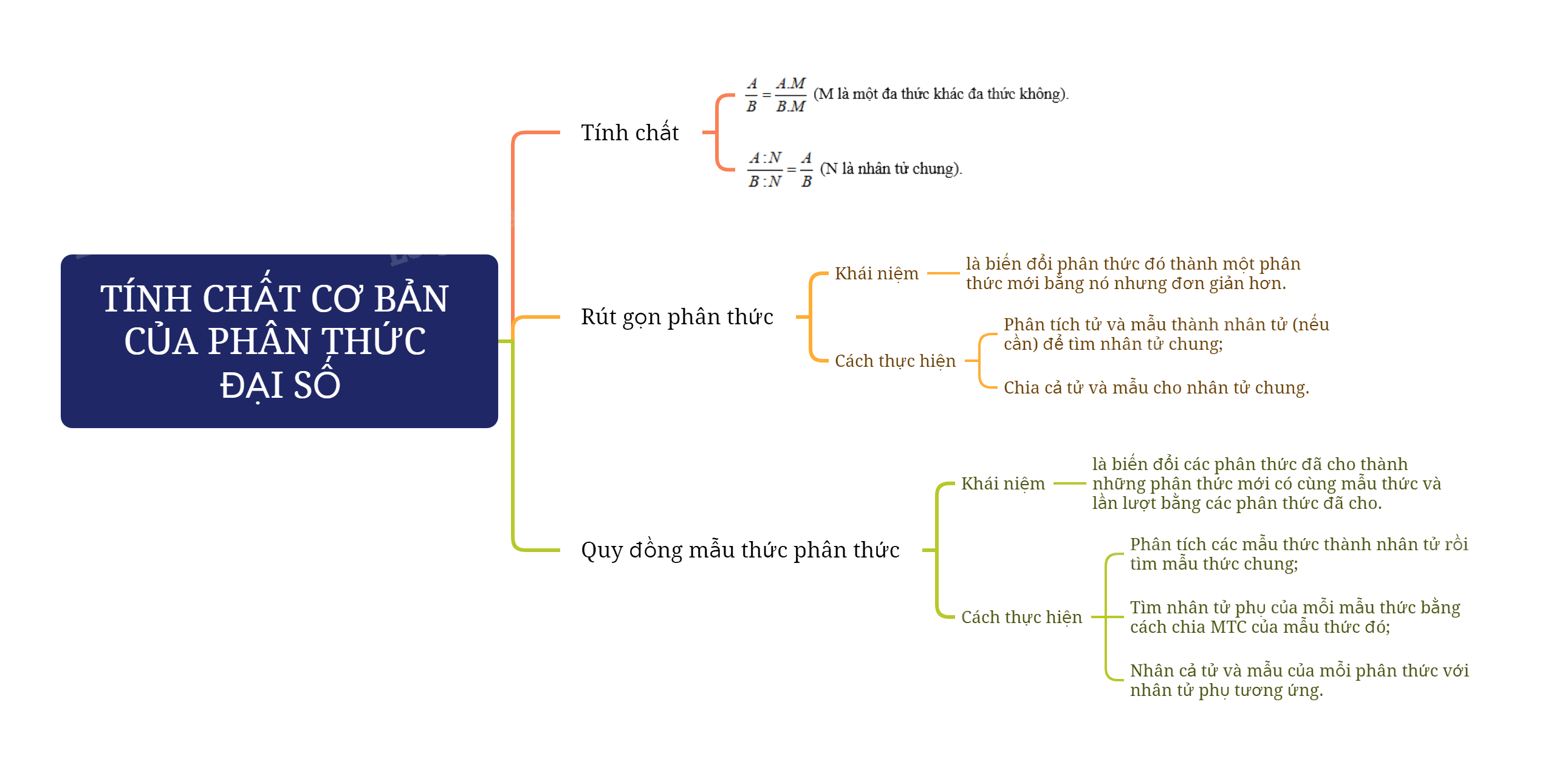
1. Tính chất cơ bản của phân thức
- Tính chất cơ bản của phân thức:
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.
\(\frac{A}{B} = \frac{{A.M}}{{B.M}}\) (M là một đa thức khác đa thức không).
Nếu chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
\(\frac{{A:N}}{{B:N}} = \frac{A}{B}\) (N là nhân tử chung).
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.
Ví dụ: Để biến đổi phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) thành \(\frac{{ - 1}}{{x + y}}\), ta chia cả tử và mẫu của phân thức \(\frac{{x - y}}{{{y^2} - {x^2}}}\) cho y – x, khi đó
\(\frac{{x - y}}{{{y^2} - {x^2}}} \\= \frac{{ - (y - x)}}{{(y - x)(y + x)}} \\= \frac{{ - 1}}{{x + y}}\)
2. Rút gọn phân thức
Rút gọn một phân thức là biến đổi phân thức đó thành một phân thức mới bằng nó nhưng đơn giản hơn.
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung;
- Chia cả tử và mẫu cho nhân tử chung.
3. Quy đồng mẫu thức nhiều phân thức
Quy đồng mẫu thức nhiều phân thức là biến đổi các phân thức đã cho thành những phân thức mới có cùng mẫu thức và lần lượt bằng các phân thức đã cho.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC của mẫu thức đó;
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
Ví dụ: Quy đồng mẫu thức hai phân thức \(\frac{1}{{{x^2} + x}}\) và \(\frac{1}{{{x^2} - x}}\)
MTC là: \(x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)\)
Ta có:
\(\left[ {x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)} \right]:\left[ {x(x + 1)} \right] = x - 1;\\\left[ {x\left( {x{\rm{ }} + {\rm{ }}1} \right)\left( {x{\rm{ }}-{\rm{ }}1} \right)} \right]:\left[ {x(x - 1)} \right] = x + 1\)
Khi đó: \(\frac{1}{{{x^2} + x}} = \frac{1}{{x(x + 1)}} = \frac{{x - 1}}{{x(x + 1)(x - 1)}};\\\frac{1}{{{x^2} - x}} = \frac{1}{{x(x - 1)}} = \frac{{x + 1}}{{x(x - 1)(x + 1)}}\)
- Quy tắc đổi dấu: Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.
$\frac{A}{B}=\frac{-A}{-B}$; $\frac{-A}{B}=\frac{A}{-B}=-\frac{A}{B}$.
Phân thức đại số là một biểu thức toán học quan trọng trong chương trình Toán 8, là nền tảng cho các kiến thức nâng cao hơn ở các lớp trên. Việc nắm vững lý thuyết và các tính chất cơ bản của phân thức đại số là điều cần thiết để giải quyết các bài toán một cách chính xác và hiệu quả.
Một phân thức đại số là một biểu thức có dạng P/Q, trong đó P và Q là các đa thức, và Q khác 0. P được gọi là tử số, Q được gọi là mẫu số.
Hai phân thức P/Q và A/B được gọi là tương đương nếu P*B = Q*A. Tính chất này cho phép chúng ta rút gọn phân thức và đơn giản hóa các biểu thức toán học.
Để đổi dấu một phân thức, ta đổi dấu cả tử và mẫu của phân thức. Ví dụ: -P/Q = P/-Q.
Để rút gọn một phân thức, ta chia cả tử và mẫu của phân thức cho ước chung lớn nhất của chúng. Ví dụ: Nếu P = 2x2 + 4x và Q = x2 + 2x, thì ước chung lớn nhất của P và Q là x(x+2). Do đó, phân thức có thể được rút gọn thành 2/(x+2).
Để cộng hoặc trừ hai phân thức, chúng ta cần quy đồng mẫu số. Sau khi quy đồng, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số chung.
Để nhân hai phân thức, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
P/Q * A/B = (P*A)/(Q*B)
Để chia hai phân thức, ta nhân phân thức thứ nhất với nghịch đảo của phân thức thứ hai.
P/Q : A/B = P/Q * B/A = (P*B)/(Q*A)
Ví dụ 1: Rút gọn phân thức 6x2/9x
Giải: Ta có 6x2 = 2 * 3 * x * x và 9x = 3 * 3 * x. Ước chung lớn nhất của 6x2 và 9x là 3x. Do đó, 6x2/9x = (2x)/3
Ví dụ 2: Thực hiện phép cộng 1/x + 2/y
Giải: Mẫu số chung là xy. Ta có 1/x + 2/y = y/xy + 2x/xy = (y+2x)/xy
Lý thuyết phân thức đại số có nhiều ứng dụng trong toán học và các lĩnh vực khác. Nó được sử dụng để giải các phương trình, bất phương trình, và các bài toán thực tế. Việc hiểu rõ các tính chất cơ bản của phân thức đại số sẽ giúp bạn giải quyết các vấn đề một cách hiệu quả hơn.
Để nắm vững lý thuyết, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn. Việc luyện tập sẽ giúp bạn hiểu sâu hơn về các khái niệm và rèn luyện kỹ năng giải toán.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Tính chất cơ bản của phân thức đại số. Chúc bạn học tốt!