Chào mừng bạn đến với bài học về lý thuyết các trường hợp đồng dạng của hai tam giác vuông trong chương trình Toán 8 Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đồng dạng tam giác, đặc biệt là các trường hợp đồng dạng của hai tam giác vuông.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, tính chất và ứng dụng thực tế của lý thuyết này.
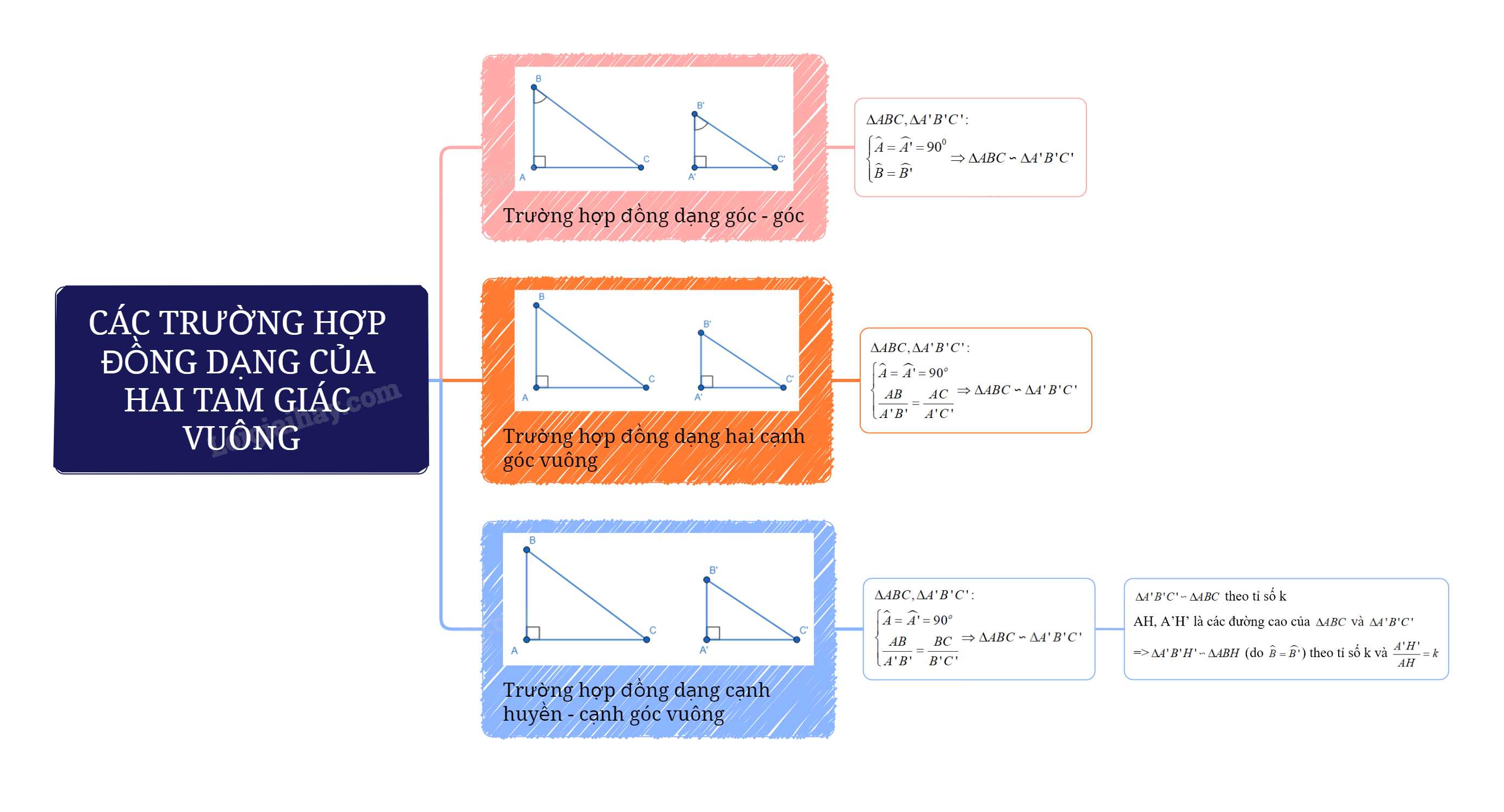
Có các trường hợp đồng dạng nào của hai tam giác vuông?
1. Trường hợp góc – góc:
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đồng dạng với nhau.
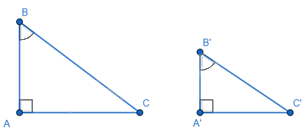
\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)
2. Trường hợp hai cạnh góc vuông:
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
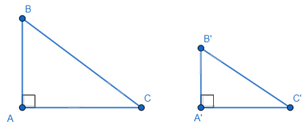
\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^o}\\\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)
3. Trường hợp cạnh huyền – cạnh góc vuông:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
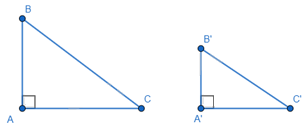
\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^o}\\\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)
Nhận xét: Nếu \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số k và AH, A’H’ lần lượt là các đường cao của \(\Delta ABC\) và \(\Delta A'B'C'\) thì \(\Delta A'B'H' \backsim \Delta ABH\) (do \(\widehat B = \widehat {B'}\)) theo tỉ số k và \(\frac{{A'H'}}{{AH}} = k\).
Trong chương trình Toán 8, phần học về tam giác đồng dạng đóng vai trò quan trọng, và việc nắm vững các trường hợp đồng dạng của hai tam giác vuông là nền tảng để giải quyết nhiều bài toán hình học phức tạp. Bài viết này sẽ trình bày chi tiết lý thuyết này, kèm theo các ví dụ minh họa và bài tập vận dụng để giúp bạn hiểu rõ hơn.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Kí hiệu: ΔABC ~ ΔA'B'C' (đọc là tam giác ABC đồng dạng với tam giác A'B'C').
Điều kiện cần và đủ để hai tam giác đồng dạng là:
Có ba trường hợp đồng dạng của hai tam giác vuông:
Nếu ΔABC vuông tại A và ΔA'B'C' vuông tại A' có ∠B = ∠B' thì ΔABC ~ ΔA'B'C'.
Chứng minh:
Vì ΔABC và ΔA'B'C' đều là tam giác vuông, nên ∠A = ∠A' = 90°. Theo giả thiết, ∠B = ∠B'. Suy ra ∠C = 180° - ∠A - ∠B = 180° - ∠A' - ∠B' = ∠C'. Vậy ΔABC ~ ΔA'B'C' (g.g).
Nếu ΔABC vuông tại A và ΔA'B'C' vuông tại A' có AB/A'B' = AC/A'C' thì ΔABC ~ ΔA'B'C'.
Chứng minh:
Xét ΔABC và ΔA'B'C'. Ta có AB/A'B' = AC/A'C' và ∠A = ∠A' = 90°. Suy ra ΔABC ~ ΔA'B'C' (c.g.c).
Nếu ΔABC vuông tại A và ΔA'B'C' vuông tại A' có BC/B'C' = AB/A'B' thì ΔABC ~ ΔA'B'C'.
Chứng minh:
Xét ΔABC và ΔA'B'C'. Ta có BC/B'C' = AB/A'B' và ∠A = ∠A' = 90°. Áp dụng định lý Pytago, ta có AC = √(BC² - AB²) và A'C' = √(B'C'² - A'B'²). Từ giả thiết, ta suy ra AC/A'C' = 1. Vậy ΔABC ~ ΔA'B'C' (c.g.c).
Các trường hợp đồng dạng của hai tam giác vuông được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là:
Ví dụ 1: Cho ΔABC vuông tại A, AB = 3cm, AC = 4cm. Cho ΔA'B'C' vuông tại A' có ∠B' = ∠B. Tính độ dài các cạnh A'B' và A'C' biết B'C' = 5cm.
Giải:
Vì ΔABC ~ ΔA'B'C' (trường hợp 1), ta có AB/A'B' = AC/A'C' = BC/B'C'. Tính BC = √(AB² + AC²) = √(3² + 4²) = 5cm. Suy ra A'B' = AB * B'C' / BC = 3 * 5 / 5 = 3cm và A'C' = AC * B'C' / BC = 4 * 5 / 5 = 4cm.
1. Cho ΔABC vuông tại A, AB = 6cm, AC = 8cm. Cho ΔA'B'C' vuông tại A' có AB/A'B' = AC/A'C'. Tính độ dài các cạnh A'B' và A'C' biết B'C' = 10cm.
2. Cho ΔABC vuông tại A, AB = 5cm, ∠B = 45°. Cho ΔA'B'C' vuông tại A' có ∠B' = ∠B. Tính độ dài các cạnh A'B' và A'C' biết B'C' = 7cm.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết các trường hợp đồng dạng của hai tam giác vuông. Chúc bạn học tốt!